Refine search
Actions for selected content:
8126 results in Fluid dynamics and solid mechanics
On the constructive approximation of non-linear operators in the modelling of dynamical systems
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 39 / Issue 1 / July 1997
- Published online by Cambridge University Press:
- 17 February 2009, pp. 1-27
-
- Article
-
- You have access
- Export citation
Stochastic maximum principle for optimal control problem of forward and backward system
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 37 / Issue 2 / October 1995
- Published online by Cambridge University Press:
- 17 February 2009, pp. 172-185
-
- Article
-
- You have access
- Export citation
Non-linear optimization of the material constants in Ogden's stress-deformation function for incompressinle isotropic elastic materials
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 24 / Issue 4 / April 1983
- Published online by Cambridge University Press:
- 17 February 2009, pp. 424-434
-
- Article
-
- You have access
- Export citation
Some remarks on Pauli data in quantum mechanics
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 30 / Issue 3 / January 1989
- Published online by Cambridge University Press:
- 17 February 2009, pp. 298-303
-
- Article
-
- You have access
- Export citation
On two lemmas of Brown and Shepp having application to sum sets and fractals, III
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 41 / Issue 3 / January 2000
- Published online by Cambridge University Press:
- 17 February 2009, pp. 329-337
-
- Article
-
- You have access
- Export citation
The generalized Shannon system in wavelet space
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 41 / Issue 3 / January 2000
- Published online by Cambridge University Press:
- 17 February 2009, pp. 386-400
-
- Article
-
- You have access
- Export citation
ANZ volume 21 issue 1 Cover and Back matter
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 21 / Issue 1 / April 1979
- Published online by Cambridge University Press:
- 17 February 2009, pp. b1-b2
-
- Article
-
- You have access
- Export citation
A reaction-diffusion model of stored bagasse
-
- Journal:
- The ANZIAM Journal / Volume 43 / Issue 1 / July 2001
- Published online by Cambridge University Press:
- 17 February 2009, pp. 13-34
-
- Article
-
- You have access
- Export citation
Exact solutions for redistribution by nonlinear convection-diffusion
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 33 / Issue 3 / January 1992
- Published online by Cambridge University Press:
- 17 February 2009, pp. 363-383
-
- Article
-
- You have access
- Export citation
Forced cubic Schrödinger equation with Robin boundary data: continuous dependency result
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 41 / Issue 3 / January 2000
- Published online by Cambridge University Press:
- 17 February 2009, pp. 301-311
-
- Article
-
- You have access
- Export citation
Critical point behaviour of the diffusion length for radiative transfer
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 27 / Issue 2 / October 1985
- Published online by Cambridge University Press:
- 17 February 2009, pp. 245-257
-
- Article
-
- You have access
- Export citation
Boundary conditions for approximate differential equations
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 34 / Issue 1 / July 1992
- Published online by Cambridge University Press:
- 17 February 2009, pp. 54-80
-
- Article
-
- You have access
- Export citation
ANZ volume 30 issue 4 Cover and Back matter
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 30 / Issue 4 / April 1989
- Published online by Cambridge University Press:
- 17 February 2009, pp. b1-b2
-
- Article
-
- You have access
- Export citation
Solution of homogeneous linear difference equations
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 21 / Issue 3 / January 1980
- Published online by Cambridge University Press:
- 17 February 2009, pp. 293-296
-
- Article
-
- You have access
- Export citation
ANZ volume 44 issue 4 Cover and Back matter
-
- Journal:
- The ANZIAM Journal / Volume 44 / Issue 4 / April 2003
- Published online by Cambridge University Press:
- 17 February 2009, pp. b1-b3
-
- Article
-
- You have access
- Export citation
Initiation of thermal explosion by intense light: criticality dependence on data and parameters
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 28 / Issue 3 / January 1987
- Published online by Cambridge University Press:
- 17 February 2009, pp. 287-295
-
- Article
-
- You have access
- Export citation
A note on the impulse due to a vapour bubble near a boundary
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 23 / Issue 4 / April 1982
- Published online by Cambridge University Press:
- 17 February 2009, pp. 383-393
-
- Article
-
- You have access
- Export citation
Integrability, random matrices and Painlevé transcendents
-
- Journal:
- The ANZIAM Journal / Volume 44 / Issue 1 / July 2002
- Published online by Cambridge University Press:
- 17 February 2009, pp. 41-50
-
- Article
-
- You have access
- Export citation
Growth and oscillation properties of solutions of a fourth order linear difference equation
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 26 / Issue 3 / January 1985
- Published online by Cambridge University Press:
- 17 February 2009, pp. 310-328
-
- Article
-
- You have access
- Export citation
Existence theorems for optimal control of quasilinear parabolic partial differential equations
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 21 / Issue 1 / April 1979
- Published online by Cambridge University Press:
- 17 February 2009, pp. 90-101
-
- Article
-
- You have access
- Export citation
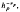 , where the critical exponent is found to be
, where the critical exponent is found to be 