Refine search
Actions for selected content:
8126 results in Fluid dynamics and solid mechanics
The numerical solution of Hammerstein equations by a method based on polynomial collocation
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 31 / Issue 3 / January 1990
- Published online by Cambridge University Press:
- 17 February 2009, pp. 319-329
-
- Article
-
- You have access
- Export citation
Some new results for the Lagrange polynomials in several variables
-
- Journal:
- The ANZIAM Journal / Volume 49 / Issue 2 / October 2007
- Published online by Cambridge University Press:
- 17 February 2009, pp. 243-258
-
- Article
-
- You have access
- Export citation
The dual reciprocity boundary element method for magnetohydrodynamic channel flows
-
- Journal:
- The ANZIAM Journal / Volume 44 / Issue 2 / October 2002
- Published online by Cambridge University Press:
- 17 February 2009, pp. 305-322
-
- Article
-
- You have access
- Export citation
ANZ volume 32 issue 2 Cover and Front matter
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 32 / Issue 2 / October 1990
- Published online by Cambridge University Press:
- 17 February 2009, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Critical initial conditions for spatially-distributed thermal explosions
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 33 / Issue 3 / January 1992
- Published online by Cambridge University Press:
- 17 February 2009, pp. 350-362
-
- Article
-
- You have access
- Export citation
ANZ volume 46 issue 4 Cover and Back matter
-
- Journal:
- The ANZIAM Journal / Volume 46 / Issue 4 / April 2005
- Published online by Cambridge University Press:
- 17 February 2009, pp. b1-b2
-
- Article
-
- You have access
- Export citation
ANZ volume 36 issue 4 Cover and Front matter
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 36 / Issue 4 / April 1995
- Published online by Cambridge University Press:
- 17 February 2009, pp. f1-f2
-
- Article
-
- You have access
- Export citation
A mathematical model and related problems of optimal management and design in a broadband integrated services network
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 31 / Issue 2 / October 1989
- Published online by Cambridge University Press:
- 17 February 2009, pp. 150-175
-
- Article
-
- You have access
- Export citation
Cyclic gravity waves in deep water
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 25 / Issue 1 / July 1983
- Published online by Cambridge University Press:
- 17 February 2009, pp. 2-15
-
- Article
-
- You have access
- Export citation
On the convergence of an iterative method for the minimax problem
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 39 / Issue 2 / October 1997
- Published online by Cambridge University Press:
- 17 February 2009, pp. 280-292
-
- Article
-
- You have access
- Export citation
ANZ volume 36 issue 3 Cover and Front matter
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 36 / Issue 3 / January 1995
- Published online by Cambridge University Press:
- 17 February 2009, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Existence theorems for Segal quantization via spectral theory in Krein space
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 24 / Issue 4 / April 1983
- Published online by Cambridge University Press:
- 17 February 2009, pp. 439-460
-
- Article
-
- You have access
- Export citation
The Lebesgue function for generalized Hermite-Fejér interpolation on the Chebyshev nodes
-
- Journal:
- The ANZIAM Journal / Volume 42 / Issue 1 / July 2000
- Published online by Cambridge University Press:
- 17 February 2009, pp. 98-109
-
- Article
-
- You have access
- Export citation
An uncoupling procedure for a class of coupled linear partial differential equations
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 26 / Issue 4 / April 1985
- Published online by Cambridge University Press:
- 17 February 2009, pp. 503-516
-
- Article
-
- You have access
- Export citation
Assessing regularised solutions
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 30 / Issue 1 / July 1988
- Published online by Cambridge University Press:
- 17 February 2009, pp. 24-42
-
- Article
-
- You have access
- Export citation
On partly bilateral and partly unilateral generating functions
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 28 / Issue 2 / October 1986
- Published online by Cambridge University Press:
- 17 February 2009, pp. 240-245
-
- Article
-
- You have access
- Export citation
Splitting least squares and collocation procedures for two-point boundary value problems
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 27 / Issue 2 / October 1985
- Published online by Cambridge University Press:
- 17 February 2009, pp. 167-193
-
- Article
-
- You have access
- Export citation
Observer-based robust H∞, control for uncertain time-delay systems
-
- Journal:
- The ANZIAM Journal / Volume 44 / Issue 4 / April 2003
- Published online by Cambridge University Press:
- 17 February 2009, pp. 625-634
-
- Article
-
- You have access
- Export citation
Second-order time discretization with finite-element method for partial integro-differential equations with a weakly singular kernel
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 40 / Issue 4 / April 1999
- Published online by Cambridge University Press:
- 17 February 2009, pp. 513-524
-
- Article
-
- You have access
- Export citation
On the acoustic scattering amplitude for a multi-layered Scatterer
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 39 / Issue 4 / April 1998
- Published online by Cambridge University Press:
- 17 February 2009, pp. 431-448
-
- Article
-
- You have access
- Export citation
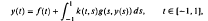
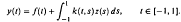
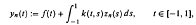
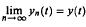 , uniformly in
, uniformly in 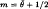 where
where 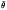 is the maximum smoothness of
is the maximum smoothness of 