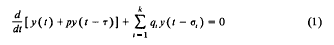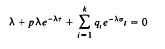Refine search
Actions for selected content:
8126 results in Fluid dynamics and solid mechanics
Controllability of generalised dynamical systems with constrained control
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 30 / Issue 1 / July 1988
- Published online by Cambridge University Press:
- 17 February 2009, pp. 69-78
-
- Article
-
- You have access
- Export citation
The elastodynamic Green's tensor for the 2D half-space
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 20 / Issue 4 / December 1978
- Published online by Cambridge University Press:
- 17 February 2009, pp. 385-400
-
- Article
-
- You have access
- Export citation
Analysis of shallow shells by a combination of finite elements and contour methods
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 32 / Issue 4 / April 1991
- Published online by Cambridge University Press:
- 17 February 2009, pp. 469-491
-
- Article
-
- You have access
- Export citation
Boundary conditions optimal control
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 30 / Issue 3 / January 1989
- Published online by Cambridge University Press:
- 17 February 2009, pp. 343-349
-
- Article
-
- You have access
- Export citation
Laplace transforms for superexponential functions
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 36 / Issue 1 / July 1994
- Published online by Cambridge University Press:
- 17 February 2009, pp. 17-25
-
- Article
-
- You have access
- Export citation
Converging factors for some asymptotic moment series that arise in numerical quadrature
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 24 / Issue 2 / October 1982
- Published online by Cambridge University Press:
- 17 February 2009, pp. 223-233
-
- Article
-
- You have access
- Export citation
Sub-supersolutions in a variational inequality related to a sandpile problem
-
- Journal:
- The ANZIAM Journal / Volume 48 / Issue 2 / October 2006
- Published online by Cambridge University Press:
- 17 February 2009, pp. 179-197
-
- Article
-
- You have access
- Export citation
Remarks on the boundary element method for strongly nonlinear problems
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 34 / Issue 4 / April 1993
- Published online by Cambridge University Press:
- 17 February 2009, pp. 419-438
-
- Article
-
- You have access
- Export citation
Speech by Professor G. C. Wake for the Professor B. F. Gray dinner
-
- Journal:
- The ANZIAM Journal / Volume 43 / Issue 1 / July 2001
- Published online by Cambridge University Press:
- 17 February 2009, pp. iv-vi
-
- Article
-
- You have access
- Export citation
On nonlinear programming and matrix game equivalence
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 35 / Issue 4 / April 1994
- Published online by Cambridge University Press:
- 17 February 2009, pp. 429-438
-
- Article
-
- You have access
- Export citation
On the generalized complementarity problem
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 35 / Issue 4 / April 1994
- Published online by Cambridge University Press:
- 17 February 2009, pp. 420-428
-
- Article
-
- You have access
- Export citation
Strongly nonlinear vortices in magnetized ferrofluids
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 40 / Issue 2 / October 1998
- Published online by Cambridge University Press:
- 17 February 2009, pp. 146-170
-
- Article
-
- You have access
- Export citation
Necessary and sufficient condition for oscillations of neutral differential equations
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 28 / Issue 3 / January 1987
- Published online by Cambridge University Press:
- 17 February 2009, pp. 362-375
-
- Article
-
- You have access
- Export citation
The deformation of rubber cylinders and tubes by rotation
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 20 / Issue 1 / June 1977
- Published online by Cambridge University Press:
- 17 February 2009, pp. 62-96
-
- Article
-
- You have access
- Export citation
Conservation laws for second-order parabolic partial differential equations
-
- Journal:
- The ANZIAM Journal / Volume 45 / Issue 3 / January 2004
- Published online by Cambridge University Press:
- 17 February 2009, pp. 333-348
-
- Article
-
- You have access
- Export citation
On an inequality relating to sum sets
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 37 / Issue 2 / October 1995
- Published online by Cambridge University Press:
- 17 February 2009, pp. 208-211
-
- Article
-
- You have access
- Export citation
ANZ volume 46 issue 2 Cover and Back matter
-
- Journal:
- The ANZIAM Journal / Volume 46 / Issue 2 / October 2004
- Published online by Cambridge University Press:
- 17 February 2009, pp. b1-b3
-
- Article
-
- You have access
- Export citation
Low Reynolds number flow in a heated tube of varying section
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 25 / Issue 2 / October 1983
- Published online by Cambridge University Press:
- 17 February 2009, pp. 244-260
-
- Article
-
- You have access
- Export citation
The inverse fractional matching problem
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 40 / Issue 4 / April 1999
- Published online by Cambridge University Press:
- 17 February 2009, pp. 484-496
-
- Article
-
- You have access
- Export citation
Guide expansions for the recursive parametric solution of polynomial dynamical systems
-
- Journal:
- The ANZIAM Journal / Volume 47 / Issue 3 / January 2006
- Published online by Cambridge University Press:
- 17 February 2009, pp. 387-396
-
- Article
-
- You have access
- Export citation
 , where μ
, where μ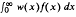 with
with