Refine search
Actions for selected content:
8126 results in Fluid dynamics and solid mechanics
Calculating the near field of a line of sources using Mellin transforms
-
- Journal:
- The ANZIAM Journal / Volume 49 / Issue 1 / July 2007
- Published online by Cambridge University Press:
- 17 February 2009, pp. 99-109
-
- Article
-
- You have access
- Export citation
Global asymptotic stability in an almost-periodic Lotka-Volterra system
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 27 / Issue 3 / January 1986
- Published online by Cambridge University Press:
- 17 February 2009, pp. 346-360
-
- Article
-
- You have access
- Export citation
The likely antecedents of improbable events: optimal search strategies
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 34 / Issue 3 / January 1993
- Published online by Cambridge University Press:
- 17 February 2009, pp. 257-273
-
- Article
-
- You have access
- Export citation
Finite element error estimates for subsonic flow
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 29 / Issue 1 / July 1987
- Published online by Cambridge University Press:
- 17 February 2009, pp. 88-102
-
- Article
-
- You have access
- Export citation
Swimming of slender fish in a non-uniform velocity field
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 19 / Issue 1 / June 1975
- Published online by Cambridge University Press:
- 17 February 2009, pp. 95-111
-
- Article
-
- You have access
- Export citation
An elementary derivation of Pontrayagin's maximum principle of optimal control theory
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 20 / Issue 2 / December 1977
- Published online by Cambridge University Press:
- 17 February 2009, pp. 142-156
-
- Article
-
- You have access
- Export citation
A scheduling problem with a simple graphical solution
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 21 / Issue 4 / April 1980
- Published online by Cambridge University Press:
- 17 February 2009, pp. 486-495
-
- Article
-
- You have access
- Export citation
Persistence and global stability in a delayed predator-prey system with Holling-type functional response
-
- Journal:
- The ANZIAM Journal / Volume 46 / Issue 1 / July 2004
- Published online by Cambridge University Press:
- 17 February 2009, pp. 121-141
-
- Article
-
- You have access
- Export citation
Green manure and nitrogenous fertilizer—a two-sector optimal-growth model
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 28 / Issue 2 / October 1986
- Published online by Cambridge University Press:
- 17 February 2009, pp. 181-201
-
- Article
-
- You have access
- Export citation
ANZ volume 44 issue 1 Cover and Back matter
-
- Journal:
- The ANZIAM Journal / Volume 44 / Issue 1 / July 2002
- Published online by Cambridge University Press:
- 17 February 2009, pp. b1-b3
-
- Article
-
- You have access
- Export citation
Some multivariable Gaussian hypergeometric extensions of the Preece theorem
-
- Journal:
- The ANZIAM Journal / Volume 48 / Issue 1 / July 2006
- Published online by Cambridge University Press:
- 17 February 2009, pp. 143-150
-
- Article
-
- You have access
- Export citation
Stochastic models for interference between searching insect parasites
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 30 / Issue 3 / January 1989
- Published online by Cambridge University Press:
- 17 February 2009, pp. 268-277
-
- Article
-
- You have access
- Export citation
ANZ volume 39 issue 3 Cover and Front matter
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 39 / Issue 3 / January 1998
- Published online by Cambridge University Press:
- 17 February 2009, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Asymptotic estimates for symmetric vortex streets
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 26 / Issue 4 / April 1985
- Published online by Cambridge University Press:
- 17 February 2009, pp. 487-502
-
- Article
-
- You have access
- Export citation
ANZ volume 43 issue 4 Cover and Front matter
-
- Journal:
- The ANZIAM Journal / Volume 43 / Issue 4 / April 2002
- Published online by Cambridge University Press:
- 17 February 2009, pp. f1-f4
-
- Article
-
- You have access
- Export citation
A transformation of Cooke's treatment of some triple integral equations
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 19 / Issue 3 / June 1976
- Published online by Cambridge University Press:
- 17 February 2009, pp. 259-288
-
- Article
-
- You have access
- Export citation
Radial flow through deformable porous shells
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 34 / Issue 3 / January 1993
- Published online by Cambridge University Press:
- 17 February 2009, pp. 333-354
-
- Article
-
- You have access
- Export citation
The wave resistance formula of J.H. Michell (1898) and Its significance to recent research in ship hydrodynamics
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 30 / Issue 4 / April 1989
- Published online by Cambridge University Press:
- 17 February 2009, pp. 365-377
-
- Article
-
- You have access
- Export citation
ANZ volume 42 issue 3 Back matter
-
- Journal:
- The ANZIAM Journal / Volume 42 / Issue 3 / January 2001
- Published online by Cambridge University Press:
- 17 February 2009, pp. b1-b2
-
- Article
-
- You have access
- Export citation
When can sigmoidal data be fit to a Hill curve?
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 41 / Issue 1 / July 1999
- Published online by Cambridge University Press:
- 17 February 2009, pp. 83-92
-
- Article
-
- You have access
- Export citation
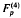 and Srivastava's quadruple hypergeometric function
and Srivastava's quadruple hypergeometric function 
