Refine search
Actions for selected content:
8126 results in Fluid dynamics and solid mechanics
ANZ volume 28 issue 1 Cover and Back matter
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 28 / Issue 1 / July 1986
- Published online by Cambridge University Press:
- 17 February 2009, pp. b1-b2
-
- Article
-
- You have access
- Export citation
Smoothly attaching bow flows with constant vorticity
-
- Journal:
- The ANZIAM Journal / Volume 42 / Issue 3 / January 2001
- Published online by Cambridge University Press:
- 17 February 2009, pp. 354-371
-
- Article
-
- You have access
- Export citation
Bubbles rising in an inclined two-dimensional tube and jets falling along a wall
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 39 / Issue 3 / January 1998
- Published online by Cambridge University Press:
- 17 February 2009, pp. 332-349
-
- Article
-
- You have access
- Export citation
The best least squares approximation problem for a 3-parametric exponential regression model
-
- Journal:
- The ANZIAM Journal / Volume 42 / Issue 2 / October 2000
- Published online by Cambridge University Press:
- 17 February 2009, pp. 254-266
-
- Article
-
- You have access
- Export citation
On generalised convex multi-objective nonsmooth programming
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 38 / Issue 1 / July 1996
- Published online by Cambridge University Press:
- 17 February 2009, pp. 140-148
-
- Article
-
- You have access
- Export citation
A solution method for combined semi-infinite and semi-definite programming
-
- Journal:
- The ANZIAM Journal / Volume 45 / Issue 4 / April 2004
- Published online by Cambridge University Press:
- 17 February 2009, pp. 477-494
-
- Article
-
- You have access
- Export citation
Harvesting in a two-prey one-predator fishery: a bioeconomic model
-
- Journal:
- The ANZIAM Journal / Volume 45 / Issue 3 / January 2004
- Published online by Cambridge University Press:
- 17 February 2009, pp. 443-456
-
- Article
-
- You have access
- Export citation
ANZ volume 20 issue 4 Cover and Back matter
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 20 / Issue 4 / December 1978
- Published online by Cambridge University Press:
- 17 February 2009, pp. b1-b2
-
- Article
-
- You have access
- Export citation
Thermodynamic limit for a system with dipole-dipole interactions
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 19 / Issue 1 / June 1975
- Published online by Cambridge University Press:
- 17 February 2009, pp. 116-128
-
- Article
-
- You have access
- Export citation
Asymptotology—a cautionary tale
-
- Journal:
- The ANZIAM Journal / Volume 44 / Issue 1 / July 2002
- Published online by Cambridge University Press:
- 17 February 2009, pp. 33-40
-
- Article
-
- You have access
- Export citation
Summing series arising from integro-differential-difference equations
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 41 / Issue 4 / April 2000
- Published online by Cambridge University Press:
- 17 February 2009, pp. 473-486
-
- Article
-
- You have access
- Export citation
Content of Volume 41
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 41 / Issue 4 / April 2000
- Published online by Cambridge University Press:
- 17 February 2009, pp. 580-582
-
- Article
-
- You have access
- Export citation
A one-dimensional random walk with repulsion
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 20 / Issue 3 / June 1978
- Published online by Cambridge University Press:
- 17 February 2009, pp. 375-380
-
- Article
-
- You have access
- Export citation
A numerical method for friction problems with multiple contacts
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 37 / Issue 3 / January 1996
- Published online by Cambridge University Press:
- 17 February 2009, pp. 288-308
-
- Article
-
- You have access
- Export citation
Flux ratios for biological membranes and reciprocity theorems for linear operators
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 30 / Issue 3 / January 1989
- Published online by Cambridge University Press:
- 17 February 2009, pp. 278-297
-
- Article
-
- You have access
- Export citation
A note on the flow induced by a line sink beneath a free surface
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 32 / Issue 3 / January 1991
- Published online by Cambridge University Press:
- 17 February 2009, pp. 251-260
-
- Article
-
- You have access
- Export citation
The foliage density equation revisited
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 27 / Issue 4 / April 1986
- Published online by Cambridge University Press:
- 17 February 2009, pp. 387-401
-
- Article
-
- You have access
- Export citation
Infinite Froude number solutions to the problem of a submerged source or sink
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 29 / Issue 4 / April 1988
- Published online by Cambridge University Press:
- 17 February 2009, pp. 401-409
-
- Article
-
- You have access
- Export citation
Nonlinear programming duality and matrix game equivalence
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 26 / Issue 4 / April 1985
- Published online by Cambridge University Press:
- 17 February 2009, pp. 422-429
-
- Article
-
- You have access
- Export citation
Elastic plastic analysis of shallow shells—a new approach
-
- Journal:
- The ANZIAM Journal / Volume 47 / Issue 1 / July 2005
- Published online by Cambridge University Press:
- 17 February 2009, pp. 121-130
-
- Article
-
- You have access
- Export citation
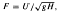 the angle β between the left wall and the horizontal, and the angle γ between the free surface and the right wall at the separation point. Numerical solutions are obtained
the angle β between the left wall and the horizontal, and the angle γ between the free surface and the right wall at the separation point. Numerical solutions are obtained 