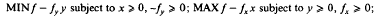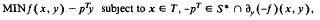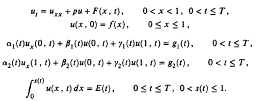Refine search
Actions for selected content:
8126 results in Fluid dynamics and solid mechanics
On the existence and sensitivity analysis of optimal catital accumulation paths in continuous time, infinite horizon models
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 30 / Issue 4 / April 1989
- Published online by Cambridge University Press:
- 17 February 2009, pp. 450-459
-
- Article
-
- You have access
- Export citation
In Memoriam: Hilary Booth
-
- Journal:
- The ANZIAM Journal / Volume 47 / Issue 1 / July 2005
- Published online by Cambridge University Press:
- 17 February 2009, p. i
-
- Article
-
- You have access
- Export citation
A note on nondifferentiable symmetric duality
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 28 / Issue 1 / July 1986
- Published online by Cambridge University Press:
- 17 February 2009, pp. 30-35
-
- Article
-
- You have access
- Export citation
Analysis of the Michaelis-Menten mechanism in an immobilised enzyme reactor
-
- Journal:
- The ANZIAM Journal / Volume 47 / Issue 2 / October 2005
- Published online by Cambridge University Press:
- 17 February 2009, pp. 173-184
-
- Article
-
- You have access
- Export citation
Duality between distant point and median of a tree network space
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 30 / Issue 3 / January 1989
- Published online by Cambridge University Press:
- 17 February 2009, pp. 304-312
-
- Article
-
- You have access
- Export citation
Comparison principles for impulsive parabolic equations with applications to models of single species growth
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 32 / Issue 4 / April 1991
- Published online by Cambridge University Press:
- 17 February 2009, pp. 382-400
-
- Article
-
- You have access
- Export citation
Aesthetic factors in geometric modelling
-
- Journal:
- The ANZIAM Journal / Volume 42 / Issue 1 / July 2000
- Published online by Cambridge University Press:
- 17 February 2009, pp. 169-180
-
- Article
-
- You have access
- Export citation
Determination of a control parameter in a parabolic partial differential equation
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 33 / Issue 2 / October 1991
- Published online by Cambridge University Press:
- 17 February 2009, pp. 149-163
-
- Article
-
- You have access
- Export citation
Nonresonance conditions and extremal solutions for first-order impulsive problems under weak assumptions
-
- Journal:
- The ANZIAM Journal / Volume 44 / Issue 3 / January 2003
- Published online by Cambridge University Press:
- 17 February 2009, pp. 393-407
-
- Article
-
- You have access
- Export citation
A note on anti-plane shear for compressible materials in finite elastostatics
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 20 / Issue 1 / June 1977
- Published online by Cambridge University Press:
- 17 February 2009, pp. 1-7
-
- Article
-
- You have access
- Export citation
Contents of Volume 39
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 39 / Issue 4 / April 1998
- Published online by Cambridge University Press:
- 17 February 2009, pp. 577-579
-
- Article
-
- You have access
- Export citation
Travelling waves in phase field models of solidification
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 36 / Issue 3 / January 1995
- Published online by Cambridge University Press:
- 17 February 2009, pp. 325-371
-
- Article
-
- You have access
- Export citation
Exact solutions of nonlinear evolution equations of the AKNS class
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 30 / Issue 3 / January 1989
- Published online by Cambridge University Press:
- 17 February 2009, pp. 313-325
-
- Article
-
- You have access
- Export citation
ANZ volume 47 issue 4 Cover and Back matter
-
- Journal:
- The ANZIAM Journal / Volume 47 / Issue 4 / April 2006
- Published online by Cambridge University Press:
- 17 February 2009, pp. b1-b2
-
- Article
-
- You have access
- Export citation
Wavelet transform of the dilation equation
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 37 / Issue 4 / April 1996
- Published online by Cambridge University Press:
- 17 February 2009, pp. 474-489
-
- Article
-
- You have access
- Export citation
ANZ volume 30 issue 2 Cover and Front matter
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 30 / Issue 2 / October 1988
- Published online by Cambridge University Press:
- 17 February 2009, pp. f1-f2
-
- Article
-
- You have access
- Export citation
The Taylor series for bandlimited signals
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 36 / Issue 1 / July 1994
- Published online by Cambridge University Press:
- 17 February 2009, pp. 101-106
-
- Article
-
- You have access
- Export citation
Closed form solution to some mixed boundary value problems for a charged sphere
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 28 / Issue 3 / January 1987
- Published online by Cambridge University Press:
- 17 February 2009, pp. 296-309
-
- Article
-
- You have access
- Export citation
Degenerate forms of Maxwell's equations
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 31 / Issue 3 / January 1990
- Published online by Cambridge University Press:
- 17 February 2009, pp. 277-300
-
- Article
-
- You have access
- Export citation
A method of accelerating stationary iterative methods for solving linear systems
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 30 / Issue 1 / July 1988
- Published online by Cambridge University Press:
- 17 February 2009, pp. 1-23
-
- Article
-
- You have access
- Export citation