The Fritz John necessary conditions for optimality of a differentiable nonlinear programming problem have been shown, given additional convexity hypotheses, to be also sufficient (by Gulati, Craven, and others). This sufficiency theorem is now extended to minimization (suitably defined) of a function taking values in a partially ordered space, and to (convex) objective and constraint functions which are not always differentiable. The results are expressed in terms of subgradients.

A list of recognised social diversities is assembled, including those used in social action programmes in the USA. Responses to diversity are discussed and diversity sensitivity defined as the derivative of response with respect to a defining parameter of a diversity distribution. Rewards (or penalties) for diversity are listed also; sensitivities to the responses to the rewards for diversity are called diversity sensitivities of the second kind. The statistics of bimodal and multimodal distributions are discussed, including the parametric estimation of such distributions by mixtures of multivariate normal distributions. An example is considered in detail.

A predator-prey model in which the prey population is subdivided into nine genotypes corresponding to a two-locus, two-allele problem is considered. Sufficient conditions are given which lead to extinction of all the prey allele types except one, as well as conditions which guarantee the persistence of all the allele types.

We investigate the strict lower subdifferentiability of a real-valued function on a closed convex subset of Rn. Relations between the strict lower subdifferential, lower subdifferential, and the usual convex subdifferential are established. Furthermore, we present necessary and sufficient optimality conditions for a class of quasiconvex minimization problems in terms of lower and strict lower subdifferentials. Finally, a descent direction method is proposed and global convergence results of the consequent algorithm are obtained.

The electrostatic field of a set of arbitrarily located circular disks is considered. A set of governing integral equations is derived by a new method. It is shown that some integral characteristics can be found without solving the integral equations. The upper and lower bounds for the total charge are found from a set of linear algebraic equations whose coefficients are defined by simple geometric characteristics of the system. Examples considered show sufficient sharpness of the estimations.

In this paper, we consider the numerical solution of a class of optimal control problems involving variable time points in their cost functions. The control enhancing transform is first used to convert the optimal control problem with variable time points into an equivalent optimal control problem with fixed multiple characteristic time (MCT). Using the control parametrization technique, the time horizon is partitioned into several subintervals. Let the partition points also be taken as decision variables. The control functions are approximated by piecewise constant or piecewise linear functions in accordance with these variable partition points. We thus obtain a finite dimensional optimization problem. The control parametrization enhancing control transform (CPET) is again used to convert approximate optimal control problems with variable partition points into equivalent standard optimal control problems with MCT, where the control functions are piecewise constant or piecewise linear functions with pre-fixed partition points. The transformed problems are essentially optimal parameter selection problems with MCT. The gradient formulae for the objective function as well as the constraint functions with respect to relevant decision variables are obtained. Numerical examples are solved using the proposed method.

The controllable set of a controlled ordinary differential dynamic system to a given set is defined. Under certain reasonable conditions, the controllable set is characterised by a level set of the unique viscosity solution to some Hamilton-Jacobi-Bellman equation. The result is used to determine the asymptotic stable set of nonlinear autonomous differential equations.

The interest in retrial queueing systems mainly lies in their application to telephone systems. This paper studies multiserver retrial queueing systems with n servers. The arrival process is a quite general point process. An arriving customer occupies one of the free servers. If upon arrival all servers are busy, then the customer waits for his service in orbit, and after a random time retries in order to occupy a server. The orbit has one waiting space only, and an arriving customer, who finds all servers busy and the waiting space occupied, is lost from the system. Time intervals between possible retrials are assumed to have arbitrary distribution (the retrial scheme is explained more precisely in the paper). The paper provides analysis of this system. Specifically the paper studies the optimal number of servers to decrease the loss proportion to a given value. The representation obtained for the loss proportion enables us to solve the problem numerically. The algorithm for numerical solution includes effective simulation, which meets the challenge of a rare events problem in simulation.

A boundary integral procedure for the solution of an important class of problems in anisotropic elasticity is outlined. Specific numerical examples are considered in order to provide a comparison with the standard boundary integral method.

The Pontryagin theory of optimal control is modified by assuming a positive cost associated with switching control from one discrete value to another. The resulting new theory permits a general existence theorem. Pontryagin's maximum principle is replaced by an “indifference principle”.

Polynomial identities for the generators of a simple basic classical Lie superalgebra are derived in arbitrary representations generated by a maximal (or minimal) weight vector. The infinitesimal characters occurring in the tensor product of two finite dimensional irreducible representations are also determined.

An analysis is made of the Daley-Kendall and Maki-Thompson rumour models starting from general initial proportions of ignorants, spreaders and stiflers in the population. We investigate as a function of the initial conditions the composition of the final population when the rumour has run its course.

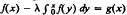Our purpose in this paper is to display the stability analysis of Runge–Kutta methods applied to a Volterra integral equation of a simple form. As prerequisite we define, and then develop the structure of, the class of Runge–Kutta methods considered. The test equation is taken as the “;basic” equation ; the simple form of this equation permits ready insight into features which are more obscure when considering (as elsewhere [1], [2], [6]) equations of a more complicated form. 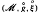Due to the structure of the methods and the nature of the test equation, the stability analysis reduces to the study of recurrence relations of the form Фk + 1 = MФ k + γk (k = 0, 1, 2, …) which are common in stability discussions in numerical analysis.

The linear long-wave equations with (and without) small ground motion are considered. The governing equations are represented in a matrix from and transformations are sought which reduce the system to (for example) a form associated with the conventional wave equation. Integration of the system is then immediate. It is shown that such a reduction may be acheived provided the variation in water depth is specified by certain multi-parameter forms.

In this paper various two-dimensional motions are determined for waves in a stratified region of infinite total depth with a free surface containing two superposed liquids, allowing for the effects of surface and interfacial tension. The fundamental set of wave-source potentials for the two layers is used to construct the set of slope potentials that produce discontinuous free-surface and interface slopes. The latter potentials are then utilized to obtain the potentials for waves due to both heaving vertical plates and incident progressive waves against a vertical wall. The underlying assumption of small time-harmonic motion pertains, described by a pair of velocity potentials for the two layers satisfying coupled linearized boundary-value problems, and all solutions are obtained in terms of their matching basic solutions. The technique for applying Green's theorem in the two layers is developed for use with the wave-source potentials, which themselves are found to obey a generalised reciprocity principle. Familiar results for a single liquid of infinite depth are hereby extended, but the new feature emerges of there being two types of progressive waves in all solutions. For ease of presentation the solutions are obtained for a particular relationship between surface and interfacial tension.

A proof is given for the existence and uniqueness of a stationary vacuum solution (M, g, ξ) of the boundary value problem consisting of Einstein's equations in an exterior domain M diffeomorphic to R × Σ (where Σ = R3\B(0, R)) and boundary data depending on the Killing field ξ on ∂Σ. The boundary data must be sufficiently close to that of a stationary, spatially conformally flat vacuum solution .

We consider a mesh grading quadrature method for real constant-coefficient Cauchy singular integral equations of index 0. The quadrature method is based on the trapezoidal rule. A complete stability and convergence analysis is given by the use of the noncompact perturbation analysis as in Jeon [10] and Elschner and Stephan [7]. The order of convergence can be arbitrarily high if the order of mesh grading is high enough. We also provide an efficient way of evaluating asymptotics of the solution at the end points. Experimentally, we observe that the method also works well for Cauchy singular integral equations with variable coefficients.

We consider the stability of high Reynolds number flow past a heated, curved wall. The influence of both buoyancy and curvature, with the appropriate sense, can render a flow unstable to longitudinal vortices. However, conversely each mechanism can make a flow more stable; as with a stable stratification or a convex curvature. This is partially due to their influence on the basic flow and also due to additional terms in the stability equations. In fact the presence of buoyancy in combination with an appropriate local wall gradient can actually increase the wall shear and these effects can lead to supervelocities and the promotion of a wall jet. This leads to the interesting discovery that the flow can be unstable for both concave and convex curvatures. Furthermore, it is possible to observe sustained vortex growth in stably stratified boundary layers over convexly curved walls. The evolution of the modes is considered in both the linear and nonlinear régimes.