In this paper we prove the existence of asymptotic expansions of the error of the spline collocation method applied to Fredholm integral equations of the first kind with logarithmic kernels. These expansions justify the use of Richardson extrapolation for the acceleration of convergence of the method. The results are stated and proven for a single equation, corresponding to the parameterization of a boundary integral equation on a smooth closed curve. As a byproduct we obtain the nodal superconvergence of the scheme. These results are then extended to smooth open arcs and to systems of integral equations. Finally we prove that such expansions also exist for the Sloan iteration of the numerical solution.

Steady state solutions for spontaneous thermal ignition in a unit sphere are considered. The multiplicity of unstable, intermediate, steady state, temperature profiles is calculated and shown for selected parameter values. The crossing of the temperature profiles corresponding to the unstable, intermediate, steady states is exhibited in a particular case and is proven in general using elementary ideas from analysis. Estimates of the location of crossing points are given.

Duffing's differential equation in its simplest form can be approximated by a variety of difference equations. It is shown how to choose a ‘best’ difference equation in the sense that the solutions of this difference equation are successive discrete exact values of the solution of the differential equation.

In this paper computational issues of Appell's F1 function

are addressed. A novel technique is used in the derivation of highly efficient multiple-term approximations of this function (including asymptotic ones). Simple structured single- and double-term approximations, as the first two candidates of this multiple-term representa-tion, are developed in closed form. Error analysis shows that- the developed algorithms are superior to existing approximations for the same number of terms. The formulation presented is highly efficient and could be extended to a wide class of special functions.

This paper is concerned with robustness with respect to small delays for the exponential stability of abstract differential equations in Banach spaces. Some necessary and sufficient conditions are given in terms of the uniformly square integrability of the fundamental operator family and the uniform boundedness of its resolvent on the imaginary axis.

Sufficient conditions are established for all solutions of the linear system

to be oscillatory, where qij ∈(−∞, ∞), τij ∈ (0, ∞), i, j = 1, 2, …, n.

The method of the Lie theory of extended groups has recently been formulated for Hamiltonian mechanics in a manner which is consistent with the results obtained using the Newtonian equation of motion. Here the method is applied to the three-dimensional time-independent harmonic oscillator and to the classical Kepler problem. The expected constants of motion are obtained. Previously unobserved relations between generators and invariants are also noticed.

We present various inequalities for Euler's beta function of n variables. One of our theorems states that the inequalities

hold for all xi ≥ (i = 1,… n; n ≥ 3) with the best possible constants an = 0 and bn = 1 − 1/(n − 1)!. This extends a recently published result of Dragomir et al., who investigated (*) for the special case n = 2.

The inverse spectral method for a general N × N spectral problem for solving nonlinear evolution equations in one spacial and one temporal dimension is extended to include multi-boundary jumps and high-order poles and their explicit representations. It therefore provides a formalism to generate soliton solutions that correspond to higher-order poles of the spectral data.

In 2002 the Mathematics in Industry Study Group (MISG) investigated the question of optimally scheduling cyclic production in a battery charging and finishing facility. The facility produces various types of battery and the scheduling objective is to maximize battery throughout subject to achieving a pre-specified product-mix. In this paper we investigate the robustness of such schedules using simulation experiments that span multiple production cycles. We simulate random variations (delays) in battery charging time and find that an optimal off-line schedule yields higher throughput in comparison to a common on-line dispatching rule. This result has been found to hold for a range of expected charging-time delays and has significant practical implications for scheduling battery charging and finishing facilities.

We study the equation

Here s is not necessarily integral; m is initially unrestricted. Material-conserving instantaneous source solutions of A are reviewed as an entrée to material-losing solutions. Simple physical arguments show that solutions for a finite slug losing material at infinity at a finite nonzero rate can exist only for the following m-ranges: 0 < s < 2, −2s−1 < m ≤ −1; s > 2, −1 < m < −2s−1. The result for s = 1 was known previously. The case s = 2, m = −1, needs further investigation. Three different similarity schemes all lead to the same ordinary differential equation. For 0 < s < 2, parameter γ (0 < γ < ∞) in that equation discriminates between the three classes of solution: class 1 gives the concentration scale decreasing as a negative power of (1 + t/T); 2 gives exponential decrease; and 3 gives decrease as a positive power of (1 − t/T), the solution vanishing at t = T < ∞. 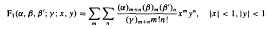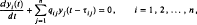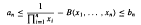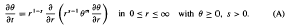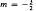Solutions for s = 1, are presented graphically. The variation of concentration and flux profiles with increasing γ is physically explicable in terms of increasing flux at infinity. An indefinitely large number of exact solutions are found for s = 1,γ = 1. These demonstrate the systematic variation of solution properties as m decreases from −1 toward −2 at fixed γ.

Wave reflection by a wedge in deep water is examined, where the wedge can represent a breakwater of finite length or the bow of a ship heading directly into the waves. In addition, the form of the solution allows the results to apply to ships heading at an angle into the waves. We consider a deep-water wavetrain approaching the wedge head on from infinity and being reflected. Far from the wedge there is a field of progressive waves (the incident wavetrain) while close to the wedge there is a short-crested wavefield (the incident and reflected wavetrains). A weakly-nonlinear slowly-varying averaged Lagrangian theory is used to describe the problem (see Whitham [16]) as the theory includes the nonlinear interaction between the incident and reflected wavetrains. This modelling of a short-crested wavefield allows the nonlinear wavefield to be found for broad wedges, as opposed to previous theories which are applicable to thin wedges only.

It is shown that the governing partial differential equations are hyperbolic and that the solution comprises two regions, within which the wave properties are constant separated by a wave jump. Given the wedge angle and the incident wavefield, the jump angle and the wave steepness and wavenumber of the short-crested wave-field behind the wave jump can be determined. Two solution branches are found to exist: one corresponds to regular reflection, while for small amplitudes the other is similar to Mach-reflection and so it is called near Mach-reflection. Results are presented describing both solution branches and the transition between them.

Recently, several papers [2–4, 6] have been published concerning a pursuit problem which was apparently first posed explicitly by Leonardo da Vinci and which may have been present in earlier thinking about kinematics and geometry. Falconry appears to go back, in Europe, to the days of Pliny, Aristotle and Martial, and, in Asia, to 2000 BC [5].

Voigt functions occur frequently in a wide variety of problems in several diverse fields of physics. This paper presents a unified study of generalised Voigt functions. In particular, some expansions of unified Voigt functions are given in terms of the original functions. Some deductions from these representations are obtained which give us an opportunity to underline the special rôle of the associated generating functions.