The algebraic structure of relativistic wave equations of the form

is considered. This leads to the problem of finding all Lie algebras L which contain the Lorentz Lie algebra so(3, 1) and also contain a “four-vector” αμ a such an L gives rise to a family of wave equations. The simplest possibility is the Bhabha equations where L≅so(5). Some authors have claimed that this is the only one, but it is shown that there are many other possibilities still in accord with physical requirements. Known facts about representations, along with Dynkin's theory of the embeddings of Lie algebras, are used to obtain a partial classification of wave equations. The discrete transformations C, P, T are also discussed, along with reality properties. Finally, a simple example of a family of wave equations based on L = sp(12) is considered in detail. The so(3, 1) content and mass spectra are given for the low order members of the family, and the problem of causality is briefly discussed.

We give an intrinsic construction of a coupled nonlinear system consisting of two first-order partial differential equations in two dependent and two independent variables which is determined by a hyperbolic structure on the complex special linear group regarded as a real Lie group G. Despite the fact that the system is not Darboux semi-integrable at first order, the construction of a family of solutions depending.upon two arbitrary functions, each of one variable, is reduced to a system of ordinary differential equations on the 1-jets. The ordinary differential equations in question are of Lie type and associated with G.

Nonlinear hydromagnetic convection in a horizontal layer of fluid rotating about the vertical axis is investigated using the mean field approximation. The boundary layer method is used assuming large Rayleigh number R for different ranges of the Chandrasekhar number Q and the Taylor number Ta. The heat flux F is determined for the value of the horizontal wave number α which maximizes F. It is shown that, for certain regions of the parameter space (R, Q, Ta), F and α change discontinuously for Ta greater than some critical value (given R and Q). Thus, for Ta about this critical value, wave numbers and heat fluxes of two different values will be predicted simultaneously. Also, for certian regions of the parameter space, the field can facilitate convection, but rotation can facilitate convection only for sufficiently large Ta.

It is shown that if intraspecific self-regulating negative feedback effects are strong enough such that a nontrivial steady state of a two species system is locally asymptotically stable, then time delays in the positive feedback as well as in other interspecific interactions cannot destabilise the system and hence delay induced instability leading to persistent oscillations is impossible whatever the magnitude of the time delays. A method is also proposed for an estimate of decay rate of perturbations.

The purpose of this paper is to study a stochastic model which assesses the effect of mutual interference on the searching efficiency in populations of insect parasites. By looking carefully at the assumptions which govern the model, I shall explain why the searching efficiency is of the same order as the total number, N, in the population, a conclusion which is consistent with the predictions of population biologists; previous studies have reached the conclusion that the efficiency is of order . 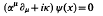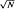The major results of the paper establish normal approximations for the distribution of the numbers of active parasites. These are valid at all stages of the process, in particular the non-equilibrium phase, where explicit analytic formulae for the state-probabilities are unavailable.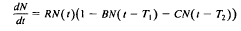

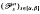Recently we have developed a completely symmetric duality theory for mathematical programming problems involving convex functionals. Here we set our theory within the framework of a Lagrangian formalism which is significantly different to the conventional Lagrangian. This allows various new characterizations of optimality.

By a systematic search for Lie-Bäetcklund symmetries, a class of linearisable reaction-diffusion equations is obtained that has, as a canonical form, ut = u2uxx + 2u2. One such nonlinear equation is θt = ∂x[a(b - θ)-2 θx] - ma(b -θ)-2 θx - q exp(-mx). This represents an extension of Fokas-Yortsos-Rosen equation (q = 0) to incorporate a reaction term. It is relevant to the modelling of unsaturated flow in a soil with a volumetric extraction mechanism, such as a web of plant roots. Here, a reciprocal transformation is used to solve a nonlinear boundary-value problem for transient flow into a finite layer of a soil subject to a constant flux boundary condition to compensate for such water extraction.

The non-linear differential difference equation of the form

is investigated. This equation, with constant coefficients, is used to model the population level, N, of a single species, and incorporates two constant time lags T2 > T1 > 0; for example, regeneration and reproductive lags. The linear equation is investigated analytically, and some linear stability regions are described. The special case in which the two delay terms are equally important in self damping, B = C, is investigated in detail. Numerical solutions for this case show stable limit cycles, with multiple loops appearing when T2/T1 is large. These may correspond to splitting of major peaks in population density observations.

In this paper a constrained Chebyshev polynomial of the second kind with C1-continuity is proposed as an error function for degree reduction of Bézier curves with a C1-constraint at both endpoints. A sharp upper bound of the L∞ norm for a constrained Chebyshev polynomial of the second kind with C1-continuity can be obtained explicitly along with its coefficients, while those of the constrained Chebyshev polynomial which provides the best C1-constrained degree reduction are obtained numerically. The representations in closed form for the coefficients and the error bound are very useful to the users of Computer Graphics or CAD/CAM systems. Using the error bound in the closed form, a simple subdivision scheme for C1-constrained degree reduction within a given tolerance is presented. As an illustration, our method is applied to C1-constrained degree reduction of a plane Bézier curve, and the numerical result is compared visually to that of the best degree reduction method.

We will study one-parameter families of differentiable optimal control problems given by: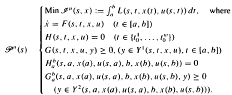

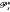Here, at given times t the inequality constraint functions are of semi-infinite nature, the objective functional may also be of max-type. For each s ∈ ℝ the problem is equivalent to a one-parameter family (Ps (t))t∈[a,b] of differentiable optimization problems. From these the consideration of generalized critical trajectories, such as a local minimum trajectory, comes into our investigation. According to a concept introduced by Hettich, Jongen and Stein in optimization, we distinguish eight types of generalized critical trajectories. Under suitable continuity, compactness and integrability assumptions, those problems, which exclusively have generalized critical points being of one of these eight types, are generic. We study normal forms and characteristic examples, locally around these trajectories.

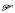Moreover, we indicate the related concept of structural stability of optimal control problems due to the topological behaviour of the lower level sets under small data perturbations. Finally, we discuss the numerical consequences of our investigations for pathfollowing techniques with jumps.

To assess rotational deformity in a broken forearm, an orthopaedic surgeon needs to determine the amount of rotation of the radius from one or more two-dimensional x-rays of the fracture. This requires only simple first-year university mathematics — rotational transformations of ellipses plus a little differential calculus — which yields a general formula giving the rotation angle from information obtained from an x-ray. Preliminary comparisons with experimental results are excellent. This is a practical problem that may be useful to motivate the teaching of conic sections.

In this paper, multigrid methods for solving the biharmonic equation using some nonconforming plate elements are considered. An average algorithm is applied to define the transfer operator. A general analysis of convergence is given.

The point form of the conservation of energy equation is used to give simple and direct proof of results concerning the mean energy flux vector for systems of sinusoidal small amplitude waves in linear conservative systems. No constitutive equation is used explicitly.

In this paper, a function involving the divided difference of the psi function is proved to be completely monotonic, a class of inequalities involving sums is found, and an equivalent relation between complete monotonicity and one of the class of inequalities is established.

Humoral immunity is that aspect of specific immunity that is mediated by B lymphocytes and involves the neutralising of disease-producing microorganisms, called pathogens, by means of antibodies attaching to the pathogen's binding sites. This inhibits the pathogen's entry into target cells. We present a master equation in both discrete and in continuous form for a ligand bound at n sites becoming a ligand bound at m sites in a given interaction time. To track the time-evolution of the antibody-ligand interaction, it is shown that the process is most easily treated classically and that in this case the master equation can be reduced to an equivalent one-dimensional diffusion equation. Thus well-known diffusion theory can be applied to antibody-ligand interactions. We consider three distinct cases depending on whether the probability of antibody binding compared to the probability of dissociation is relatively large, small or comparable, and numerical solutions are given.

An approximate solution is determined for the problem of scattering of water waves by a nearly vertical plate, by reducing it to two mixed boundary-value problems (BVP) for Laplace's equation, using perturbation techniques. While the solution of one of these BVP is well-known, the other BVPs is reduced to the problem of solving two uncoupled problems, and the complete solution of the problem under consideration up to first-order accuracy is derived with a special assumption on the shape of the plate and a related approximation. Known results involving the reflection and transmission coefficients are reproduced.