Refine search
Actions for selected content:
8126 results in Fluid dynamics and solid mechanics
ANZ volume 43 issue 3 Cover and Front matter
-
- Journal:
- The ANZIAM Journal / Volume 43 / Issue 3 / January 2002
- Published online by Cambridge University Press:
- 17 February 2009, pp. f1-f4
-
- Article
-
- You have access
- Export citation
Synthesis of layered shells from a finite set of viscoelastic materials
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 40 / Issue 4 / April 1999
- Published online by Cambridge University Press:
- 17 February 2009, pp. 525-534
-
- Article
-
- You have access
- Export citation
Two infinite-Froude-number cusped free-surface flows due to a submerged line source or sink
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 28 / Issue 2 / October 1986
- Published online by Cambridge University Press:
- 17 February 2009, pp. 260-270
-
- Article
-
- You have access
- Export citation
General iterative methods for nonlinear boundary value problems
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 37 / Issue 1 / July 1995
- Published online by Cambridge University Press:
- 17 February 2009, pp. 58-85
-
- Article
-
- You have access
- Export citation
Eigenvalue characterization for (n · p) boundary-value problems
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 39 / Issue 3 / January 1998
- Published online by Cambridge University Press:
- 17 February 2009, pp. 386-407
-
- Article
-
- You have access
- Export citation
Numerical integration of the RLW equation using cubic splines
-
- Journal:
- The ANZIAM Journal / Volume 47 / Issue 1 / July 2005
- Published online by Cambridge University Press:
- 17 February 2009, pp. 131-142
-
- Article
-
- You have access
- Export citation
Series operations using minimum storage
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 21 / Issue 1 / April 1979
- Published online by Cambridge University Press:
- 17 February 2009, pp. 84-89
-
- Article
-
- You have access
- Export citation
The commutation relation i[Y, Z] = 2Y and the absolutely continuous spectrum of Y
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 23 / Issue 4 / April 1982
- Published online by Cambridge University Press:
- 17 February 2009, pp. 420-427
-
- Article
-
- You have access
- Export citation
The sputtering temperature of a cooling cylindrical rod without and with an insulated core in a two-fluid medium
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 38 / Issue 1 / July 1996
- Published online by Cambridge University Press:
- 17 February 2009, pp. 87-100
-
- Article
-
- You have access
- Export citation
The transition through resonance of a nonlinear non-autonomous system
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 34 / Issue 1 / July 1992
- Published online by Cambridge University Press:
- 17 February 2009, pp. 81-111
-
- Article
-
- You have access
- Export citation
A robust linearisation scheme for a nonlinear elliptic boundary value problem: Error estimates
-
- Journal:
- The ANZIAM Journal / Volume 46 / Issue 4 / April 2005
- Published online by Cambridge University Press:
- 17 February 2009, pp. 449-470
-
- Article
-
- You have access
- Export citation
Computer-controlled variable-structure systems
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 34 / Issue 1 / July 1992
- Published online by Cambridge University Press:
- 17 February 2009, pp. 1-17
-
- Article
-
- You have access
- Export citation
New algorithms for discrete-time optimal control problems
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 26 / Issue 2 / October 1984
- Published online by Cambridge University Press:
- 17 February 2009, pp. 129-145
-
- Article
-
- You have access
- Export citation
Geomatric ergodicity and quasi-stationarity in discrete-time birth-death processes
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 37 / Issue 2 / October 1995
- Published online by Cambridge University Press:
- 17 February 2009, pp. 121-144
-
- Article
-
- You have access
- Export citation
Optimal control problems with elastic collisions
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 30 / Issue 4 / April 1989
- Published online by Cambridge University Press:
- 17 February 2009, pp. 470-482
-
- Article
-
- You have access
- Export citation
Derivation of the probability density function for ultimate muscle pH in slaughtered animals
-
- Journal:
- The ANZIAM Journal / Volume 45 / Issue 1 / July 2003
- Published online by Cambridge University Press:
- 17 February 2009, pp. 27-34
-
- Article
-
- You have access
- Export citation
ANZ volume 40 issue 3 Cover and Front matter
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 40 / Issue 3 / January 1999
- Published online by Cambridge University Press:
- 17 February 2009, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Growth estimates for solutions of nonlinear second-order difference equations
-
- Journal:
- The ANZIAM Journal / Volume 46 / Issue 3 / January 2005
- Published online by Cambridge University Press:
- 17 February 2009, pp. 439-448
-
- Article
-
- You have access
- Export citation
A representation result for two-input two-output decentralized control systems
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 21 / Issue 1 / April 1979
- Published online by Cambridge University Press:
- 17 February 2009, pp. 113-127
-
- Article
-
- You have access
- Export citation
Sequential eigenfunction expansion for a problem in combustion theory
-
- Journal:
- The ANZIAM Journal / Volume 45 / Issue 1 / July 2003
- Published online by Cambridge University Press:
- 17 February 2009, pp. 35-48
-
- Article
-
- You have access
- Export citation
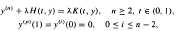
 on
on 