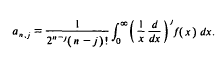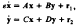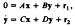Refine search
Actions for selected content:
8126 results in Fluid dynamics and solid mechanics
ANZ volume 30 issue 4 Cover and Front matter
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 30 / Issue 4 / April 1989
- Published online by Cambridge University Press:
- 17 February 2009, pp. f1-f3
-
- Article
-
- You have access
- Export citation
Scattering of water waves by a submerged thin vertical wall with a gap
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 39 / Issue 3 / January 1998
- Published online by Cambridge University Press:
- 17 February 2009, pp. 318-331
-
- Article
-
- You have access
- Export citation
Patient-dependent effects in disease control: a mathematical model
-
- Journal:
- The ANZIAM Journal / Volume 48 / Issue 4 / April 2007
- Published online by Cambridge University Press:
- 17 February 2009, pp. 583-596
-
- Article
-
- You have access
- Export citation
ANZ volume 34 issue 1 Cover and Back matter
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 34 / Issue 1 / July 1992
- Published online by Cambridge University Press:
- 17 February 2009, pp. b1-b2
-
- Article
-
- You have access
- Export citation
ANZ volume 23 issue 4 Cover and Front matter
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 23 / Issue 4 / April 1982
- Published online by Cambridge University Press:
- 17 February 2009, pp. f1-f2
-
- Article
-
- You have access
- Export citation
The control parameterization enhancing transform for constrained optimal control problems
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 40 / Issue 3 / January 1999
- Published online by Cambridge University Press:
- 17 February 2009, pp. 314-335
-
- Article
-
- You have access
- Export citation
Flow in the porous region between slowly rotating prolate spheroids
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 22 / Issue 3 / January 1981
- Published online by Cambridge University Press:
- 17 February 2009, pp. 284-290
-
- Article
-
- You have access
- Export citation
Nonlinearly constrained optimal control problems involving piecewise smooth controls
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 32 / Issue 2 / October 1990
- Published online by Cambridge University Press:
- 17 February 2009, pp. 151-179
-
- Article
-
- You have access
- Export citation
Non-Newtonian conducting fluid flow and heat transfer due to a rotating disk
-
- Journal:
- The ANZIAM Journal / Volume 46 / Issue 2 / October 2004
- Published online by Cambridge University Press:
- 17 February 2009, pp. 237-248
-
- Article
-
- You have access
- Export citation
Subgradient representation of multifunctions
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 40 / Issue 3 / January 1999
- Published online by Cambridge University Press:
- 17 February 2009, pp. 301-313
-
- Article
-
- You have access
- Export citation
The asymptotic response of a calorimeter
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 22 / Issue 3 / January 1981
- Published online by Cambridge University Press:
- 17 February 2009, pp. 348-352
-
- Article
-
- You have access
- Export citation
Oscillation of symplectic dynamic systems
-
- Journal:
- The ANZIAM Journal / Volume 46 / Issue 1 / July 2004
- Published online by Cambridge University Press:
- 17 February 2009, pp. 17-32
-
- Article
-
- You have access
- Export citation
Contents of Volume 34
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 34 / Issue 4 / April 1993
- Published online by Cambridge University Press:
- 17 February 2009, pp. 523-524
-
- Article
-
- You have access
- Export citation
Flowshop/no-idle scheduling to minimise the mean flowtime
-
- Journal:
- The ANZIAM Journal / Volume 47 / Issue 2 / October 2005
- Published online by Cambridge University Press:
- 17 February 2009, pp. 265-275
-
- Article
-
- You have access
- Export citation
ANZ volume 29 issue 3 Cover and Back matter
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 29 / Issue 3 / January 1988
- Published online by Cambridge University Press:
- 17 February 2009, pp. b1-b2
-
- Article
-
- You have access
- Export citation
Ship bows with contiunous and splashless flow attachment
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 27 / Issue 4 / April 1986
- Published online by Cambridge University Press:
- 17 February 2009, pp. 442-452
-
- Article
-
- You have access
- Export citation
Two-dimensional resonators with small openings
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 24 / Issue 1 / July 1982
- Published online by Cambridge University Press:
- 17 February 2009, pp. 2-27
-
- Article
-
- You have access
- Export citation
Inversion of the Struve transform of half integer order
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 25 / Issue 2 / October 1983
- Published online by Cambridge University Press:
- 17 February 2009, pp. 161-174
-
- Article
-
- You have access
- Export citation
Stiff systems of ordinary differential equations. III. Partially stiff systems
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 23 / Issue 3 / January 1982
- Published online by Cambridge University Press:
- 17 February 2009, pp. 310-331
-
- Article
-
- You have access
- Export citation
A convergence theorem for singular integral equations
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 22 / Issue 4 / April 1981
- Published online by Cambridge University Press:
- 17 February 2009, pp. 539-552
-
- Article
-
- You have access
- Export citation
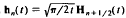 we show that the Struve transform of half integer order, or spherical Struve transform,
we show that the Struve transform of half integer order, or spherical Struve transform,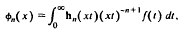
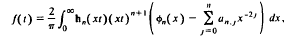
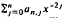 is the sum of the first
is the sum of the first