Refine search
Actions for selected content:
8126 results in Fluid dynamics and solid mechanics
Diagonal scaling of stiffness matrices in the Galerkin boundary element method
-
- Journal:
- The ANZIAM Journal / Volume 42 / Issue 1 / July 2000
- Published online by Cambridge University Press:
- 17 February 2009, pp. 141-150
-
- Article
-
- You have access
- Export citation
Optimality and duality in continuous-time nonlinear fractional programming
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 34 / Issue 2 / October 1992
- Published online by Cambridge University Press:
- 17 February 2009, pp. 229-244
-
- Article
-
- You have access
- Export citation
Solvability of generalized nonlinear symmetric variational inequalities
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 40 / Issue 3 / January 1999
- Published online by Cambridge University Press:
- 17 February 2009, pp. 289-300
-
- Article
-
- You have access
- Export citation
Generalized Hadamard's inequalities based on general Euler 4-point formulae
-
- Journal:
- The ANZIAM Journal / Volume 48 / Issue 3 / January 2007
- Published online by Cambridge University Press:
- 17 February 2009, pp. 387-404
-
- Article
-
- You have access
- Export citation
An analysis of a fractal Michaelis-Menten curve
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 41 / Issue 3 / January 2000
- Published online by Cambridge University Press:
- 17 February 2009, pp. 410-422
-
- Article
-
- You have access
- Export citation
On the geometry of the Painlevé V equation and a Bäcklund transformation
-
- Journal:
- The ANZIAM Journal / Volume 44 / Issue 1 / July 2002
- Published online by Cambridge University Press:
- 17 February 2009, pp. 141-148
-
- Article
-
- You have access
- Export citation
Properties of propagation of quantum spin systems
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 19 / Issue 4 / December 1976
- Published online by Cambridge University Press:
- 17 February 2009, pp. 387-399
-
- Article
-
- You have access
- Export citation
ANZ volume 23 issue 3 Cover and Front matter
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 23 / Issue 3 / January 1982
- Published online by Cambridge University Press:
- 17 February 2009, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Concentric circular misfit and a circular arc crack in an infinite isotropic elastic plate
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 19 / Issue 2 / December 1975
- Published online by Cambridge University Press:
- 17 February 2009, pp. 215-228
-
- Article
-
- You have access
- Export citation
Simple examples of the derivation of amplitude equations for systems of equations possessing bifurcations
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 27 / Issue 1 / July 1985
- Published online by Cambridge University Press:
- 17 February 2009, pp. 48-65
-
- Article
-
- You have access
- Export citation
Source solutions for the nonlinear diffusion-convection equation
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 39 / Issue 1 / July 1997
- Published online by Cambridge University Press:
- 17 February 2009, pp. 28-45
-
- Article
-
- You have access
- Export citation
ANZ volume 25 issue 4 Cover and Front matter
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 25 / Issue 4 / April 1984
- Published online by Cambridge University Press:
- 17 February 2009, pp. f1-f2
-
- Article
-
- You have access
- Export citation
The first integrals and their Lie algebra of the most general autonomous Hamiltonian of the form H = T + V possessing a Laplace-Runge-Lenz vector
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 34 / Issue 4 / April 1993
- Published online by Cambridge University Press:
- 17 February 2009, pp. 511-522
-
- Article
-
- You have access
- Export citation
Some remarks on relative stability
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 19 / Issue 1 / June 1975
- Published online by Cambridge University Press:
- 17 February 2009, pp. 112-115
-
- Article
-
- You have access
- Export citation
A trace formula for schrödinger operators with step potentials
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 24 / Issue 2 / October 1982
- Published online by Cambridge University Press:
- 17 February 2009, pp. 138-159
-
- Article
-
- You have access
- Export citation
A note on the random walk model arising in double diffusion
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 24 / Issue 2 / October 1982
- Published online by Cambridge University Press:
- 17 February 2009, pp. 121-129
-
- Article
-
- You have access
- Export citation
ANZ volume 44 issue 4 Cover and Front matter
-
- Journal:
- The ANZIAM Journal / Volume 44 / Issue 4 / April 2003
- Published online by Cambridge University Press:
- 17 February 2009, pp. f1-f4
-
- Article
-
- You have access
- Export citation
Some elementary exact channel flows
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 24 / Issue 4 / April 1983
- Published online by Cambridge University Press:
- 17 February 2009, pp. 484-491
-
- Article
-
- You have access
- Export citation
Adaptive boundary-element methods for transmission problems
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 38 / Issue 3 / January 1997
- Published online by Cambridge University Press:
- 17 February 2009, pp. 336-367
-
- Article
-
- You have access
- Export citation
Markov decision programming–the moment optimal problem for the first-passage model
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 38 / Issue 4 / April 1997
- Published online by Cambridge University Press:
- 17 February 2009, pp. 542-562
-
- Article
-
- You have access
- Export citation
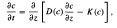
 The Poisson bracket of the two components of this vector leads to a third first-integral, cubic in the momenta. The Lie algebra of the three integrals under the operation of the Poisson bracket closes, and is shown to be
The Poisson bracket of the two components of this vector leads to a third first-integral, cubic in the momenta. The Lie algebra of the three integrals under the operation of the Poisson bracket closes, and is shown to be 