Refine search
Actions for selected content:
8126 results in Fluid dynamics and solid mechanics
Global attractivity of a class of delay differential equations with impulses
-
- Journal:
- The ANZIAM Journal / Volume 45 / Issue 2 / October 2003
- Published online by Cambridge University Press:
- 17 February 2009, pp. 271-284
-
- Article
-
- You have access
- Export citation
ANZ volume 29 issue 4 Cover and Front matter
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 29 / Issue 4 / April 1988
- Published online by Cambridge University Press:
- 17 February 2009, pp. f1-f2
-
- Article
-
- You have access
- Export citation
On Charwat's theory of motion of tracers in planar vortex flows
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 25 / Issue 2 / October 1983
- Published online by Cambridge University Press:
- 17 February 2009, pp. 175-189
-
- Article
-
- You have access
- Export citation
Contents of Volume 31
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 31 / Issue 4 / April 1990
- Published online by Cambridge University Press:
- 17 February 2009, pp. 493-494
-
- Article
-
- You have access
- Export citation
A note on the solution of the one-dimensional unsteady equations of arterial blood flow by the method of characteristics
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 21 / Issue 1 / April 1979
- Published online by Cambridge University Press:
- 17 February 2009, pp. 45-52
-
- Article
-
- You have access
- Export citation
Computing optimal control With a hyperbolic partial differential equation
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 40 / Issue 2 / October 1998
- Published online by Cambridge University Press:
- 17 February 2009, pp. 266-287
-
- Article
-
- You have access
- Export citation
On the low frequency asymptotics for the 2-D electromagnetic transmission problem
-
- Journal:
- The ANZIAM Journal / Volume 47 / Issue 3 / January 2006
- Published online by Cambridge University Press:
- 17 February 2009, pp. 397-411
-
- Article
-
- You have access
- Export citation
An interior point method for linear programming
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 31 / Issue 4 / April 1990
- Published online by Cambridge University Press:
- 17 February 2009, pp. 367-378
-
- Article
-
- You have access
- Export citation
Control in W2(1) of nonlinear interconnected systems of neutral type
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 36 / Issue 3 / January 1995
- Published online by Cambridge University Press:
- 17 February 2009, pp. 286-312
-
- Article
-
- You have access
- Export citation
Pointwise bounds for a solution of a nonlinear boundary value problem in partial differential equations
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 24 / Issue 4 / April 1983
- Published online by Cambridge University Press:
- 17 February 2009, pp. 366-373
-
- Article
-
- You have access
- Export citation
ANZ volume 28 issue 4 Cover and Front matter
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 28 / Issue 4 / April 1987
- Published online by Cambridge University Press:
- 17 February 2009, pp. f1-f2
-
- Article
-
- You have access
- Export citation
A reverse Hölder type inequality for the logarithmic mean and generalizations
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 41 / Issue 3 / January 2000
- Published online by Cambridge University Press:
- 17 February 2009, pp. 401-409
-
- Article
-
- You have access
- Export citation
Generalized multi-peg tower of hanoi problem
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 38 / Issue 2 / October 1996
- Published online by Cambridge University Press:
- 17 February 2009, pp. 201-208
-
- Article
-
- You have access
- Export citation
Evolution equations having conservation laws with flux characteristics
-
- Journal:
- The ANZIAM Journal / Volume 49 / Issue 1 / July 2007
- Published online by Cambridge University Press:
- 17 February 2009, pp. 39-52
-
- Article
-
- You have access
- Export citation
Apparent horizons in vacuum Robinson-Trautman spacetimes
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 41 / Issue 2 / October 1999
- Published online by Cambridge University Press:
- 17 February 2009, pp. 217-230
-
- Article
-
- You have access
- Export citation
ANZ volume 31 issue 2 Cover and Back matter
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 31 / Issue 2 / October 1989
- Published online by Cambridge University Press:
- 17 February 2009, pp. b1-b2
-
- Article
-
- You have access
- Export citation
Lipschitz stability of impulsive functional-differential equations
-
- Journal:
- The ANZIAM Journal / Volume 42 / Issue 4 / April 2001
- Published online by Cambridge University Press:
- 17 February 2009, pp. 504-514
-
- Article
-
- You have access
- Export citation
Subsonic potential flow past a circle and the transonic controversy
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 24 / Issue 3 / January 1983
- Published online by Cambridge University Press:
- 17 February 2009, pp. 243-261
-
- Article
-
- You have access
- Export citation
Robust stability of impulsive switched systems with disturbance
-
- Journal:
- The ANZIAM Journal / Volume 48 / Issue 2 / October 2006
- Published online by Cambridge University Press:
- 17 February 2009, pp. 259-270
-
- Article
-
- You have access
- Export citation
On monotonicity and superadditivity properties of the entropy function
-
- Journal:
- The ANZIAM Journal / Volume 42 / Issue 4 / April 2001
- Published online by Cambridge University Press:
- 17 February 2009, pp. 515-531
-
- Article
-
- You have access
- Export citation
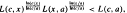
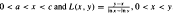 . Then several generalizations are given.
. Then several generalizations are given.