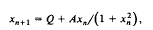Refine search
Actions for selected content:
8126 results in Fluid dynamics and solid mechanics
Refinements of some bounds in information theory
-
- Journal:
- The ANZIAM Journal / Volume 42 / Issue 3 / January 2001
- Published online by Cambridge University Press:
- 17 February 2009, pp. 387-398
-
- Article
-
- You have access
- Export citation
Hypercircle estimates for nonlinear problems
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 21 / Issue 3 / January 1980
- Published online by Cambridge University Press:
- 17 February 2009, pp. 330-337
-
- Article
-
- You have access
- Export citation
Bounds for the growth of a perturbation in some double-diffusive convection problems
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 25 / Issue 2 / October 1983
- Published online by Cambridge University Press:
- 17 February 2009, pp. 276-285
-
- Article
-
- You have access
- Export citation
ANZ volume 43 issue 1 Cover and Back matter
-
- Journal:
- The ANZIAM Journal / Volume 43 / Issue 1 / July 2001
- Published online by Cambridge University Press:
- 17 February 2009, pp. b1-b3
-
- Article
-
- You have access
- Export citation
The asymptotic behaviour due to a piecewise time dependent net maternity function
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 23 / Issue 4 / April 1982
- Published online by Cambridge University Press:
- 17 February 2009, pp. 438-450
-
- Article
-
- You have access
- Export citation
Stochastic stability of linear systems with semi-Markovian jump parameters
-
- Journal:
- The ANZIAM Journal / Volume 46 / Issue 3 / January 2005
- Published online by Cambridge University Press:
- 17 February 2009, pp. 331-340
-
- Article
-
- You have access
- Export citation
How Brian Gray became a combustion scientist
-
- Journal:
- The ANZIAM Journal / Volume 43 / Issue 1 / July 2001
- Published online by Cambridge University Press:
- 17 February 2009, pp. ii-iii
-
- Article
-
- You have access
- Export citation
Monotonicity properties of the zeros of Bessel functions
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 24 / Issue 1 / July 1982
- Published online by Cambridge University Press:
- 17 February 2009, pp. 67-85
-
- Article
-
- You have access
- Export citation
Some integral inequalities with bounds for moments of distribution II
-
- Journal:
- The ANZIAM Journal / Volume 42 / Issue 2 / October 2000
- Published online by Cambridge University Press:
- 17 February 2009, pp. 267-276
-
- Article
-
- You have access
- Export citation
Investigating semi-infinite programs using penalty functions and Lagrangian methods
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 28 / Issue 2 / October 1986
- Published online by Cambridge University Press:
- 17 February 2009, pp. 158-169
-
- Article
-
- You have access
- Export citation
On stability and stationary points in nonlinear optimization
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 28 / Issue 1 / July 1986
- Published online by Cambridge University Press:
- 17 February 2009, pp. 36-56
-
- Article
-
- You have access
- Export citation
ANZ volume 38 issue 4 Cover and Back matter
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 38 / Issue 4 / April 1997
- Published online by Cambridge University Press:
- 17 February 2009, pp. b1-b2
-
- Article
-
- You have access
- Export citation
ANZ Volume 49 Issue 1 Cover and Back matter
-
- Journal:
- The ANZIAM Journal / Volume 49 / Issue 1 / July 2007
- Published online by Cambridge University Press:
- 17 February 2009, pp. b1-b3
-
- Article
-
- You have access
- Export citation
Continuity properties of attractors for iterated fuzzy set systems
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 36 / Issue 2 / October 1994
- Published online by Cambridge University Press:
- 17 February 2009, pp. 175-193
-
- Article
-
- You have access
- Export citation
ANZ volume 35 issue 4 Cover and Back matter
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 35 / Issue 4 / April 1994
- Published online by Cambridge University Press:
- 17 February 2009, pp. b1-b2
-
- Article
-
- You have access
- Export citation
Critical values for a nonlinear difference equation
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 28 / Issue 3 / January 1987
- Published online by Cambridge University Press:
- 17 February 2009, pp. 340-361
-
- Article
-
- You have access
- Export citation
Flow fields associated with in situ mineral leaching
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 36 / Issue 2 / October 1994
- Published online by Cambridge University Press:
- 17 February 2009, pp. 133-151
-
- Article
-
- You have access
- Export citation
ANZ volume 46 issue 3 Cover and Back matter
-
- Journal:
- The ANZIAM Journal / Volume 46 / Issue 3 / January 2005
- Published online by Cambridge University Press:
- 17 February 2009, pp. b1-b3
-
- Article
-
- You have access
- Export citation
Entry flow in a straight circular pipe
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 24 / Issue 1 / July 1982
- Published online by Cambridge University Press:
- 17 February 2009, pp. 59-66
-
- Article
-
- You have access
- Export citation
An ordinary differential equation arising in the Ricci flow on the plane
-
- Journal:
- The ANZIAM Journal / Volume 42 / Issue 3 / January 2001
- Published online by Cambridge University Press:
- 17 February 2009, pp. 438-444
-
- Article
-
- You have access
- Export citation
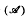 that, given the Mangasarian-Fromovitz constraint qualification (MFCQ), the feasible set
that, given the Mangasarian-Fromovitz constraint qualification (MFCQ), the feasible set 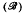 under a stability condition, two lower level sets of
under a stability condition, two lower level sets of