Refine search
Actions for selected content:
8126 results in Fluid dynamics and solid mechanics
Inertial manifold for a reaction diffusion equation model of competition in a chemostat
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 33 / Issue 1 / July 1991
- Published online by Cambridge University Press:
- 17 February 2009, pp. 9-15
-
- Article
-
- You have access
- Export citation
Robust guaranteed cost control for descriptor systems with Markov jumping parameters and state delays
-
- Journal:
- The ANZIAM Journal / Volume 47 / Issue 4 / April 2006
- Published online by Cambridge University Press:
- 17 February 2009, pp. 569-580
-
- Article
-
- You have access
- Export citation
On the dynamic analysis of a Leontief model with fixed capitial
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 27 / Issue 4 / April 1986
- Published online by Cambridge University Press:
- 17 February 2009, pp. 473-487
-
- Article
-
- You have access
- Export citation
The BMAP/G/1 vacation queue with queue-length dependent vacation schedule
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 40 / Issue 2 / October 1998
- Published online by Cambridge University Press:
- 17 February 2009, pp. 207-221
-
- Article
-
- You have access
- Export citation
Contents of Volume 25
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 25 / Issue 4 / April 1984
- Published online by Cambridge University Press:
- 17 February 2009, pp. 563-564
-
- Article
-
- You have access
- Export citation
Bifurcation phenomena for an oxidation reaction in a continuously stirred tank reactor. II Diabatic operation
-
- Journal:
- The ANZIAM Journal / Volume 45 / Issue 3 / January 2004
- Published online by Cambridge University Press:
- 17 February 2009, pp. 303-326
-
- Article
-
- You have access
- Export citation
Degree reduction of Bezier curves and its error analysis
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 36 / Issue 4 / April 1995
- Published online by Cambridge University Press:
- 17 February 2009, pp. 399-413
-
- Article
-
- You have access
- Export citation
ANZ volume 26 issue 4 Cover and Front matter
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 26 / Issue 4 / April 1985
- Published online by Cambridge University Press:
- 17 February 2009, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Subharmonic orbits in an anharmonic oscillator
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 38 / Issue 3 / January 1997
- Published online by Cambridge University Press:
- 17 February 2009, pp. 307-315
-
- Article
-
- You have access
- Export citation
Integro-differential equations for the self-organisation of liver zones by competitive exclusion of cell-types
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 29 / Issue 2 / October 1987
- Published online by Cambridge University Press:
- 17 February 2009, pp. 156-194
-
- Article
-
- You have access
- Export citation
ANZ volume 45 issue 4 Cover and Front matter
-
- Journal:
- The ANZIAM Journal / Volume 45 / Issue 4 / April 2004
- Published online by Cambridge University Press:
- 17 February 2009, pp. f1-f4
-
- Article
-
- You have access
- Export citation
ANZ volume 36 issue 1 Cover and Front matter
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 36 / Issue 1 / July 1994
- Published online by Cambridge University Press:
- 17 February 2009, pp. f1-f2
-
- Article
-
- You have access
- Export citation
An investigation into the effects of heat transfer on the motion of a spherical bubble
-
- Journal:
- The ANZIAM Journal / Volume 45 / Issue 3 / January 2004
- Published online by Cambridge University Press:
- 17 February 2009, pp. 361-371
-
- Article
-
- You have access
- Export citation
Stability in paradigm biological systems
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 40 / Issue 1 / July 1998
- Published online by Cambridge University Press:
- 17 February 2009, pp. 23-34
-
- Article
-
- You have access
- Export citation
Normal shock reflection-transmission in rubber-like elastic material
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 31 / Issue 1 / July 1989
- Published online by Cambridge University Press:
- 17 February 2009, pp. 29-47
-
- Article
-
- You have access
- Export citation
A variation-of-constants formula for a linear abstract evolution equation in Hilbert space
-
- Journal:
- The ANZIAM Journal / Volume 44 / Issue 4 / April 2003
- Published online by Cambridge University Press:
- 17 February 2009, pp. 583-590
-
- Article
-
- You have access
- Export citation
Analytical and numerical results for flow and shock formation in two-layer gravity currents
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 40 / Issue 1 / July 1998
- Published online by Cambridge University Press:
- 17 February 2009, pp. 35-58
-
- Article
-
- You have access
- Export citation
Solution of general inhomogeneous linear difference equations
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 24 / Issue 4 / April 1983
- Published online by Cambridge University Press:
- 17 February 2009, pp. 466-472
-
- Article
-
- You have access
- Export citation
An integral equation for immiscible fluid isplacement in a two-dimensional porous medium or Hele-Shaw cell
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 26 / Issue 1 / July 1984
- Published online by Cambridge University Press:
- 17 February 2009, pp. 14-30
-
- Article
-
- You have access
- Export citation
Linearised evaporation about a shallow half-plane pond
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 34 / Issue 3 / January 1993
- Published online by Cambridge University Press:
- 17 February 2009, pp. 355-367
-
- Article
-
- You have access
- Export citation
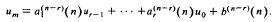
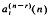 ,
, 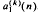 ,
, 