Refine search
Actions for selected content:
8126 results in Fluid dynamics and solid mechanics
ANZ volume 44 issue 3 Cover and Front matter
-
- Journal:
- The ANZIAM Journal / Volume 44 / Issue 3 / January 2003
- Published online by Cambridge University Press:
- 17 February 2009, pp. f1-f4
-
- Article
-
- You have access
- Export citation
Existence and regularity results for Maxwell's equations in the quasi-static limit
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 27 / Issue 4 / April 1986
- Published online by Cambridge University Press:
- 17 February 2009, pp. 402-415
-
- Article
-
- You have access
- Export citation
Stiff systems of ordinary differential equations: II. Boundary-value problems for completely stiff systems
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 23 / Issue 2 / October 1981
- Published online by Cambridge University Press:
- 17 February 2009, pp. 136-172
-
- Article
-
- You have access
- Export citation
A notion of local proper efficiency in the Borwein sense in vector optimisation
-
- Journal:
- The ANZIAM Journal / Volume 45 / Issue 1 / July 2003
- Published online by Cambridge University Press:
- 17 February 2009, pp. 75-89
-
- Article
-
- You have access
- Export citation
The application of centre-manifold theory to the evolution of system which vary slowly in space
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 29 / Issue 4 / April 1988
- Published online by Cambridge University Press:
- 17 February 2009, pp. 480-500
-
- Article
-
- You have access
- Export citation
ANZ volume 44 issue 2 Cover and Front matter
-
- Journal:
- The ANZIAM Journal / Volume 44 / Issue 2 / October 2002
- Published online by Cambridge University Press:
- 17 February 2009, pp. f1-f4
-
- Article
-
- You have access
- Export citation
Similarity solutions of the steady state cosmic-ray equation of transport
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 19 / Issue 4 / December 1976
- Published online by Cambridge University Press:
- 17 February 2009, pp. 432-451
-
- Article
-
- You have access
- Export citation
Reflection of oblique shock waves in incompressible elastic solids
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 27 / Issue 1 / July 1985
- Published online by Cambridge University Press:
- 17 February 2009, pp. 31-47
-
- Article
-
- You have access
- Export citation
ANZ volume 27 issue 3 Cover and Back matter
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 27 / Issue 3 / January 1986
- Published online by Cambridge University Press:
- 17 February 2009, pp. b1-b2
-
- Article
-
- You have access
- Export citation
Chaotic breakdown of a periodically forced, weakly damped pendulum
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 34 / Issue 2 / October 1992
- Published online by Cambridge University Press:
- 17 February 2009, pp. 153-173
-
- Article
-
- You have access
- Export citation
Steady states of the reaction-diffusion equations. Part 1: Questions of existence and continuity of solution branches
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 24 / Issue 4 / April 1983
- Published online by Cambridge University Press:
- 17 February 2009, pp. 374-391
-
- Article
-
- You have access
- Export citation
The Hadamard product of two Brownian matrices: Analytic inverse and determinant
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 36 / Issue 4 / April 1995
- Published online by Cambridge University Press:
- 17 February 2009, pp. 493-497
-
- Article
-
- You have access
- Export citation
ANZ volume 33 issue 3 Cover and Front matter
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 33 / Issue 3 / January 1992
- Published online by Cambridge University Press:
- 17 February 2009, pp. f1-f2
-
- Article
-
- You have access
- Export citation
ANZ volume 35 issue 4 Cover and Front matter
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 35 / Issue 4 / April 1994
- Published online by Cambridge University Press:
- 17 February 2009, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Generalized functions for applications
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 26 / Issue 3 / January 1985
- Published online by Cambridge University Press:
- 17 February 2009, pp. 362-374
-
- Article
-
- You have access
- Export citation
On a connection between the generalized incomplete gamma functions and their extensions
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 38 / Issue 4 / April 1997
- Published online by Cambridge University Press:
- 17 February 2009, pp. 581-589
-
- Article
-
- You have access
- Export citation
ANZ volume 20 issue 1 Cover and Front matter
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 20 / Issue 1 / June 1977
- Published online by Cambridge University Press:
- 17 February 2009, pp. f1-f2
-
- Article
-
- You have access
- Export citation
ANZ volume 41 issue 2 Cover and Front matter
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 41 / Issue 2 / October 1999
- Published online by Cambridge University Press:
- 17 February 2009, pp. f1-f3
-
- Article
-
- You have access
- Export citation
A boundary value problem for second-order nonlinear difference equations on the integers
-
- Journal:
- The ANZIAM Journal / Volume 47 / Issue 2 / October 2005
- Published online by Cambridge University Press:
- 17 February 2009, pp. 237-248
-
- Article
-
- You have access
- Export citation
Dynamics of rapid extinction in a lumped system with Arrhenius chemistry
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 23 / Issue 3 / January 1982
- Published online by Cambridge University Press:
- 17 February 2009, pp. 278-290
-
- Article
-
- You have access
- Export citation
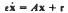
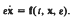
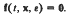
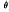 ) phase space of one or other of the two forms of periodic oscillations, where θ(
) phase space of one or other of the two forms of periodic oscillations, where θ(