Refine search
Actions for selected content:
8126 results in Fluid dynamics and solid mechanics
Early quasi-steady electro-magnetic fields about conducting surfaces
-
- Journal:
- The ANZIAM Journal / Volume 42 / Issue 4 / April 2001
- Published online by Cambridge University Press:
- 17 February 2009, pp. 481-493
-
- Article
-
- You have access
- Export citation
ANZ volume 25 issue 4 Cover and Back matter
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 25 / Issue 4 / April 1984
- Published online by Cambridge University Press:
- 17 February 2009, p. b1
-
- Article
-
- You have access
- Export citation
Gradient algorithms for principal component analysis
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 37 / Issue 4 / April 1996
- Published online by Cambridge University Press:
- 17 February 2009, pp. 430-450
-
- Article
-
- You have access
- Export citation
Nonnegative solutions for a heterogeneous degenerate competition model
-
- Journal:
- The ANZIAM Journal / Volume 46 / Issue 2 / October 2004
- Published online by Cambridge University Press:
- 17 February 2009, pp. 273-297
-
- Article
-
- You have access
- Export citation
ANZ volume 38 issue 4 Cover and Front matter
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 38 / Issue 4 / April 1997
- Published online by Cambridge University Press:
- 17 February 2009, pp. f1-f2
-
- Article
-
- You have access
- Export citation
An evolutionary monotone follower problem in [0, 1]
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 31 / Issue 1 / July 1989
- Published online by Cambridge University Press:
- 17 February 2009, pp. 97-107
-
- Article
-
- You have access
- Export citation
The structure of solutions for equations related to the motions of plane curves
-
- Journal:
- The ANZIAM Journal / Volume 45 / Issue 4 / April 2004
- Published online by Cambridge University Press:
- 17 February 2009, pp. 585-592
-
- Article
-
- You have access
- Export citation
Monotonicity of the error term in Gauss-Turán quadratures for analytic function
-
- Journal:
- The ANZIAM Journal / Volume 48 / Issue 4 / April 2007
- Published online by Cambridge University Press:
- 17 February 2009, pp. 567-581
-
- Article
-
- You have access
- Export citation
Isospectral flows and linear programming
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 34 / Issue 4 / April 1993
- Published online by Cambridge University Press:
- 17 February 2009, pp. 495-510
-
- Article
-
- You have access
- Export citation
Summing a common type of slowly convergent series of positive terms
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 19 / Issue 4 / December 1976
- Published online by Cambridge University Press:
- 17 February 2009, pp. 416-421
-
- Article
-
- You have access
- Export citation
ANZ volume 23 issue 4 Cover and Back matter
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 23 / Issue 4 / April 1982
- Published online by Cambridge University Press:
- 17 February 2009, pp. b1-b2
-
- Article
-
- You have access
- Export citation
Derivatives of addition theorems for Legendre functions
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 37 / Issue 2 / October 1995
- Published online by Cambridge University Press:
- 17 February 2009, pp. 212-234
-
- Article
-
- You have access
- Export citation
On the application of a numerical algorithm for Hopf bifuraction to the hunting of a wheelset
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 25 / Issue 3 / January 1984
- Published online by Cambridge University Press:
- 17 February 2009, pp. 384-405
-
- Article
-
- You have access
- Export citation
Generalized fractional programming duablity: a ratio game approach
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 28 / Issue 2 / October 1986
- Published online by Cambridge University Press:
- 17 February 2009, pp. 170-180
-
- Article
-
- You have access
- Export citation
ANZ volume 38 issue 3 Cover and Back matter
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 38 / Issue 3 / January 1997
- Published online by Cambridge University Press:
- 17 February 2009, pp. b1-b2
-
- Article
-
- You have access
- Export citation
Observability-enhanced proportional navigation guidance with bearings-only measurements
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 40 / Issue 4 / April 1999
- Published online by Cambridge University Press:
- 17 February 2009, pp. 497-512
-
- Article
-
- You have access
- Export citation
ANZ volume 26 issue 2 Cover and Front matter
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 26 / Issue 2 / October 1984
- Published online by Cambridge University Press:
- 17 February 2009, pp. f1-f2
-
- Article
-
- You have access
- Export citation
On the integrability and exact solutions of the nonlinear diffusion equation with a nonlinear source
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 39 / Issue 4 / April 1998
- Published online by Cambridge University Press:
- 17 February 2009, pp. 513-527
-
- Article
-
- You have access
- Export citation
Plane poloidal-toroidal decomposition of doubly periodic vector fields. Part 1. Fields with divergence
-
- Journal:
- The ANZIAM Journal / Volume 47 / Issue 1 / July 2005
- Published online by Cambridge University Press:
- 17 February 2009, pp. 21-38
-
- Article
-
- You have access
- Export citation
ANZ volume 45 issue 2 Cover and Back matter
-
- Journal:
- The ANZIAM Journal / Volume 45 / Issue 2 / October 2003
- Published online by Cambridge University Press:
- 17 February 2009, pp. b1-b2
-
- Article
-
- You have access
- Export citation
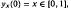 , solutions of
, solutions of 