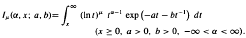Refine search
Actions for selected content:
8126 results in Fluid dynamics and solid mechanics
Approximate solutions for coupled moment equations
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 24 / Issue 1 / July 1982
- Published online by Cambridge University Press:
- 17 February 2009, pp. 86-97
-
- Article
-
- You have access
- Export citation
ANZ volume 26 issue 3 Cover and Front matter
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 26 / Issue 3 / January 1985
- Published online by Cambridge University Press:
- 17 February 2009, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Bifurcation phenomena for an oxidation reaction in a continuously stirred tank reactor. III The inhibiting effect of an inert species
-
- Journal:
- The ANZIAM Journal / Volume 46 / Issue 3 / January 2005
- Published online by Cambridge University Press:
- 17 February 2009, pp. 399-416
-
- Article
-
- You have access
- Export citation
ANZ volume 33 issue 4 Cover and Back matter
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 33 / Issue 4 / April 1992
- Published online by Cambridge University Press:
- 17 February 2009, pp. b1-b2
-
- Article
-
- You have access
- Export citation
On representations of a generalized method of field quantization
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 23 / Issue 1 / July 1981
- Published online by Cambridge University Press:
- 17 February 2009, pp. 52-63
-
- Article
-
- You have access
- Export citation
Conditions for permanence in well-known biological competition models
-
- Journal:
- The ANZIAM Journal / Volume 42 / Issue 2 / October 2000
- Published online by Cambridge University Press:
- 17 February 2009, pp. 195-223
-
- Article
-
- You have access
- Export citation
Controllability of neutral Volterra integrodifferential systems
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 34 / Issue 1 / July 1992
- Published online by Cambridge University Press:
- 17 February 2009, pp. 18-25
-
- Article
-
- You have access
- Export citation
Optimisation in the regularisation ill-posed problems
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 28 / Issue 1 / July 1986
- Published online by Cambridge University Press:
- 17 February 2009, pp. 114-133
-
- Article
-
- You have access
- Export citation
An analysis of a fractal kinetics curve of Savageau
-
- Journal:
- The ANZIAM Journal / Volume 45 / Issue 2 / October 2003
- Published online by Cambridge University Press:
- 17 February 2009, pp. 261-269
-
- Article
-
- You have access
- Export citation
The temporal evolution of a system in combustion theory
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 24 / Issue 4 / April 1983
- Published online by Cambridge University Press:
- 17 February 2009, pp. 473-483
-
- Article
-
- You have access
- Export citation
Dual barrier functions with superfast rates of convergence for the linear programming problem
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 29 / Issue 1 / July 1987
- Published online by Cambridge University Press:
- 17 February 2009, pp. 39-58
-
- Article
-
- You have access
- Export citation
Tracking control of linear switched systems
-
- Journal:
- The ANZIAM Journal / Volume 49 / Issue 2 / October 2007
- Published online by Cambridge University Press:
- 17 February 2009, pp. 187-203
-
- Article
-
- You have access
- Export citation
An analysis of local energy and phase congruency models in visual feature detection
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 40 / Issue 1 / July 1998
- Published online by Cambridge University Press:
- 17 February 2009, pp. 97-122
-
- Article
-
- You have access
- Export citation
Reflection of water waves in the presence of surface tension by a nearly vertical porous wall
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 39 / Issue 3 / January 1998
- Published online by Cambridge University Press:
- 17 February 2009, pp. 308-317
-
- Article
-
- You have access
- Export citation
The existence of periodic and subharmonic solutions to subquadratic discrete Hamiltonian systems
-
- Journal:
- The ANZIAM Journal / Volume 47 / Issue 1 / July 2005
- Published online by Cambridge University Press:
- 17 February 2009, pp. 89-102
-
- Article
-
- You have access
- Export citation
On a family of logarithmic and exponential integrals occurring in probability and reliability theory
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 35 / Issue 4 / April 1994
- Published online by Cambridge University Press:
- 17 February 2009, pp. 469-478
-
- Article
-
- You have access
- Export citation
A note on integral representations in Stokes flow
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 19 / Issue 2 / December 1975
- Published online by Cambridge University Press:
- 17 February 2009, pp. 161-164
-
- Article
-
- You have access
- Export citation
ANZ volume 39 issue 1 Cover and Front matter
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 39 / Issue 1 / July 1997
- Published online by Cambridge University Press:
- 17 February 2009, pp. f1-f2
-
- Article
-
- You have access
- Export citation
On the influence of the initial data in a combustion problem
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 22 / Issue 2 / October 1980
- Published online by Cambridge University Press:
- 17 February 2009, pp. 193-209
-
- Article
-
- You have access
- Export citation
Robust H∞ stabilisation with definite attenuance of an uncertain impulsive switche system
-
- Journal:
- The ANZIAM Journal / Volume 46 / Issue 4 / April 2005
- Published online by Cambridge University Press:
- 17 February 2009, pp. 471-484
-
- Article
-
- You have access
- Export citation