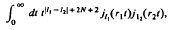Refine search
Actions for selected content:
8126 results in Fluid dynamics and solid mechanics
On the stability of solutions for the p(x)-Laplacian equation and some applications to optimisation problems with state constraints
-
- Journal:
- The ANZIAM Journal / Volume 48 / Issue 2 / October 2006
- Published online by Cambridge University Press:
- 17 February 2009, pp. 245-257
-
- Article
-
- You have access
- Export citation
Non-classical integrals of Bessel functions
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 22 / Issue 3 / January 1981
- Published online by Cambridge University Press:
- 17 February 2009, pp. 368-378
-
- Article
-
- You have access
- Export citation
ANZ volume 48 issue 4 Cover and Back matter
-
- Journal:
- The ANZIAM Journal / Volume 48 / Issue 4 / April 2007
- Published online by Cambridge University Press:
- 17 February 2009, pp. b1-b2
-
- Article
-
- You have access
- Export citation
Fourth-order nonlinear evolution equations for surface gravity waves in the presence of a thin thermocline
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 39 / Issue 2 / October 1997
- Published online by Cambridge University Press:
- 17 February 2009, pp. 214-229
-
- Article
-
- You have access
- Export citation
Accelerated spectral refinement Part I: simple eigenvalue
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 41 / Issue 4 / April 2000
- Published online by Cambridge University Press:
- 17 February 2009, pp. 487-507
-
- Article
-
- You have access
- Export citation
Stability of large-scale systems with lagged interconnections
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 21 / Issue 4 / April 1980
- Published online by Cambridge University Press:
- 17 February 2009, pp. 496-509
-
- Article
-
- You have access
- Export citation
ANZ volume 48 issue 3 Cover and Front matter
-
- Journal:
- The ANZIAM Journal / Volume 48 / Issue 3 / January 2007
- Published online by Cambridge University Press:
- 17 February 2009, pp. f1-f4
-
- Article
-
- You have access
- Export citation
Extending the utility of perturbation series in problems of laminar flow in a porous pipe and a diverging channel
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 41 / Issue 1 / July 1999
- Published online by Cambridge University Press:
- 17 February 2009, pp. 118-128
-
- Article
-
- You have access
- Export citation
ANZ volume 24 issue 1 Cover and Back matter
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 24 / Issue 1 / July 1982
- Published online by Cambridge University Press:
- 17 February 2009, pp. b1-b2
-
- Article
-
- You have access
- Export citation
Uncertainty principles invariant under the fractional Fourier transform
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 33 / Issue 2 / October 1991
- Published online by Cambridge University Press:
- 17 February 2009, pp. 180-191
-
- Article
-
- You have access
- Export citation
Growth theorems for homogeneous second-order difference equations
-
- Journal:
- The ANZIAM Journal / Volume 43 / Issue 4 / April 2002
- Published online by Cambridge University Press:
- 17 February 2009, pp. 559-566
-
- Article
-
- You have access
- Export citation
Nonlinear evolution of singular disturbances to a tanh3y mixing layer
-
- Journal:
- The ANZIAM Journal / Volume 43 / Issue 3 / January 2002
- Published online by Cambridge University Press:
- 17 February 2009, pp. 409-427
-
- Article
-
- You have access
- Export citation
ANZ volume 40 issue 3 Cover and Back matter
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 40 / Issue 3 / January 1999
- Published online by Cambridge University Press:
- 17 February 2009, pp. b1-b2
-
- Article
-
- You have access
- Export citation
Rolling of a rigid ball on a horizontal deformable surface
-
- Journal:
- The ANZIAM Journal / Volume 46 / Issue 2 / October 2004
- Published online by Cambridge University Press:
- 17 February 2009, pp. 249-264
-
- Article
-
- You have access
- Export citation
Asymptotic behaviour of a nonautonomous cooperative system
-
- Journal:
- The ANZIAM Journal / Volume 42 / Issue 4 / April 2001
- Published online by Cambridge University Press:
- 17 February 2009, pp. 561-568
-
- Article
-
- You have access
- Export citation
ANZ volume 20 issue 2 Cover and Front matter
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 20 / Issue 2 / December 1977
- Published online by Cambridge University Press:
- 17 February 2009, pp. f1-f2
-
- Article
-
- You have access
- Export citation
On competition between modes at the onset of Bénard-Marangoni convection in a layer of fluid
-
- Journal:
- The ANZIAM Journal / Volume 43 / Issue 3 / January 2002
- Published online by Cambridge University Press:
- 17 February 2009, pp. 387-395
-
- Article
-
- You have access
- Export citation
ANZ volume 28 issue 2 Cover and Back matter
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 28 / Issue 2 / October 1986
- Published online by Cambridge University Press:
- 17 February 2009, pp. b1-b2
-
- Article
-
- You have access
- Export citation
Some high-order zero-finding methods using almost orthogonal polynomials
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 19 / Issue 1 / June 1975
- Published online by Cambridge University Press:
- 17 February 2009, pp. 1-29
-
- Article
-
- You have access
- Export citation
Preface to this Volume
-
- Journal:
- The ANZIAM Journal / Volume 42 / Issue 1 / July 2000
- Published online by Cambridge University Press:
- 17 February 2009, p. 1
-
- Article
-
- You have access
- Export citation