Refine search
Actions for selected content:
8126 results in Fluid dynamics and solid mechanics
ANZ volume 22 issue 3 Cover and Back matter
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 22 / Issue 3 / January 1981
- Published online by Cambridge University Press:
- 17 February 2009, pp. b1-b2
-
- Article
-
- You have access
- Export citation
The pressure field in the gas-lubricated step slider bearing
-
- Journal:
- The ANZIAM Journal / Volume 45 / Issue 3 / January 2004
- Published online by Cambridge University Press:
- 17 February 2009, pp. 423-442
-
- Article
-
- You have access
- Export citation
ANZ volume 24 issue 3 Cover and Back matter
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 24 / Issue 3 / January 1983
- Published online by Cambridge University Press:
- 17 February 2009, pp. b1-b2
-
- Article
-
- You have access
- Export citation
A numerical scheme for the electromagnetic response in thin conductors of arbitrary planar shape
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 35 / Issue 4 / April 1994
- Published online by Cambridge University Press:
- 17 February 2009, pp. 479-497
-
- Article
-
- You have access
- Export citation
Reflection/refraction of SH-waves at a corrugated interface between two different anisotropic and vertically heterogeneous elastic solid half-spaces
-
- Journal:
- The ANZIAM Journal / Volume 44 / Issue 3 / January 2003
- Published online by Cambridge University Press:
- 17 February 2009, pp. 447-460
-
- Article
-
- You have access
- Export citation
A comparative study of smoothing approximations
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 38 / Issue 2 / October 1996
- Published online by Cambridge University Press:
- 17 February 2009, pp. 194-200
-
- Article
-
- You have access
- Export citation
Control of a surface of discontinuity in continuous thickness
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 33 / Issue 3 / January 1992
- Published online by Cambridge University Press:
- 17 February 2009, pp. 269-289
-
- Article
-
- You have access
- Export citation
Comparison and linearized oscillation theorems for a nonlinear partial difference equation
-
- Journal:
- The ANZIAM Journal / Volume 42 / Issue 4 / April 2001
- Published online by Cambridge University Press:
- 17 February 2009, pp. 552-560
-
- Article
-
- You have access
- Export citation
ANZ volume 34 issue 2 Cover and Front matter
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 34 / Issue 2 / October 1992
- Published online by Cambridge University Press:
- 17 February 2009, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Piecewise constant collocation for first-kind boundary integral equations
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 35 / Issue 3 / January 1994
- Published online by Cambridge University Press:
- 17 February 2009, pp. 396-398
-
- Article
-
- You have access
- Export citation
Long wavelength vortices in time-periodic flows
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 39 / Issue 4 / April 1998
- Published online by Cambridge University Press:
- 17 February 2009, pp. 498-512
-
- Article
-
- You have access
- Export citation
A note on continuation methods for the solution of nonlinear equations
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 20 / Issue 2 / December 1977
- Published online by Cambridge University Press:
- 17 February 2009, pp. 157-164
-
- Article
-
- You have access
- Export citation
Thermal ignition in a reactive slab with unsymmetric boundary temperatures
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 24 / Issue 3 / January 1983
- Published online by Cambridge University Press:
- 17 February 2009, pp. 279-288
-
- Article
-
- You have access
- Export citation
Splash formation at the nose of a smoothly curved body in a stream
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 40 / Issue 4 / April 1999
- Published online by Cambridge University Press:
- 17 February 2009, pp. 421-436
-
- Article
-
- You have access
- Export citation
Hearing the shape of an annular drum
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 24 / Issue 4 / April 1983
- Published online by Cambridge University Press:
- 17 February 2009, pp. 435-438
-
- Article
-
- You have access
- Export citation
The computational approach to commuting ordinary differential operators of orders six and nine
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 35 / Issue 4 / April 1994
- Published online by Cambridge University Press:
- 17 February 2009, pp. 399-419
-
- Article
-
- You have access
- Export citation
General projection systems and relaxed cocoercive nonlinear variational inequalities
-
- Journal:
- The ANZIAM Journal / Volume 49 / Issue 2 / October 2007
- Published online by Cambridge University Press:
- 17 February 2009, pp. 205-212
-
- Article
-
- You have access
- Export citation
ANZ volume 37 issue 1 Cover and Front matter
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 37 / Issue 1 / July 1995
- Published online by Cambridge University Press:
- 17 February 2009, pp. f1-f2
-
- Article
-
- You have access
- Export citation
A note on American options with varying exercise price
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 37 / Issue 1 / July 1995
- Published online by Cambridge University Press:
- 17 February 2009, pp. 45-57
-
- Article
-
- You have access
- Export citation
Blowup properties for several diffusion systems with localised sources
-
- Journal:
- The ANZIAM Journal / Volume 48 / Issue 1 / July 2006
- Published online by Cambridge University Press:
- 17 February 2009, pp. 37-56
-
- Article
-
- You have access
- Export citation
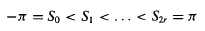
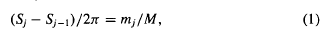
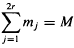 . Then γ(
. Then γ(