This note generalises the necessary and sufficient conditions for one act to be dominated by another when the two acts available to the decision maker have outcomes contingent on discrete states of nature whose probabilities of occurrence are known only to the extent of linear partial information. The generalisation relates to the dominance of an act by a set of acts. The presentation is in terms of general vector dominance, of which statistical dominance is only a particular case.

Exact wave-height solutions are presented for trapped waves over two new three-parameter depth topographies. Dispersive properties are calculated for both a semi-infinite and a truncated convex exponential profile, as well as for a semi-infinite concave profile. The analysis in all three cases is general in that both horizontal divergence and rotational effects are included. These solutions may be used for either high-frequency edge wave or low-frequency shelf wave studies by taking appropriate limits (f → 0 for edge wave and ε = f2L2/gH ≪ 1 for shelf waves).

It is shown in this note that the supremum and infimum of all causal topologies on Minkowski space are not causal. It is further shown that maximal and minimal elements exist in the set of all principal causal spaces.

We consider the phase-locked solutions of the differential equation governing planar motion of a weakly damped pendulum driven by horizontal, periodic forcing of the pivot with maximum acceleration εg and dimensionless frequency ω. Analytical solutions for symmetric oscillations at smaller values of ε are continued into numerical solutions at larger values of ε. A wide range of stable oscillatory solutions is described, including motion that is symmetric or asymmetric, downward or inverted, and at periods equal to the forcing period T ≡ 2π/ω or integral multiples thereof. Stable running oscillations with mean angular velocity pω/q, where p and q are integers, are investigated also. Stability boundaries are calculated for swinging oscillations of period T, 2T and 4T; 3T and 6T; and for running oscillations with mean angular velocity ω. The period-doubling cascades typically culminate in nearly periodic motion followed by chaotic motion or some independent periodic motion.

Four different kinds of positive asymptotic series are identified by the limiting ratio of successive terms. When the limiting ratio is 1 the series is unsummable. When the ratio tends rapidly to a constant, whether greater or less than 1, the series is easily summed. When the ratio tends slowly to a constant not equal to 1 the series is compared with a binomial model which is then used to speed the convergence. When the ratio increases linearly, a limiting binomial and an exponential integral model are both used to speed convergence. The two resulting model sums are consistent and in this case are complex numbers. Truncation at the smallest term is found to be unreliable in the second case, invalid in the third case, and the exponential integral is used to produce a significantly improved truncation in the third case. A divergent series from quantum mechanics is also examined.

A simple model for a problem in combustion theory has multiple steady state solutions when a parameter is in a certain range. This note deals with the initial value problem when the initial temperature takes the form of a hot spot. Estimates on the extent and temperature of the spot for the steady state solution to be super-critical are obtained.

We present new exact solutions for the flow of liquid during constant-rate expression from a finite thickness of liquid-saturated porous material with nonlinear properties. By varying a single nonlinearity parameter and a dimensionless expression rate, we systematically investigate the effect of nonlinearity and of an impermeable barrier (e.g. a piston). We illustrate the water profile shape and the water ratio deficit at the expression surface (e.g. a filter membrane) as a function of time.

After formulating the alternate potential principle for the nonlinear differential equation corresponding to the generalised Emden-Fowler equation, the invariance identities of Rund [14] involving the Lagrangian and the generators of the infinitesimal Lie group are used for writing down the first integrals of the said equation via the Noether theorem. Further, for physical realisable forms of the parameters involved and through repeated application of invariance under the transformation obtained, a number of exact solutions are arrived at both for the Emden-Fowler equation and classical Emden equations. A comparative study with Bluman-Cole and scale-invariant techniques reveals quite a number of remarkable features of the techniques used here.

The modulation of short gravity waves by long waves or currents is described for the situation when the flow is irrotational and when the short waves are described by linearised equations. Two cases are distinguished depending on whether the basic flow can be characterised as a deep-water current, or a shallow-water current. In both cases the basic flow has a current which has finite amplitude, while in the first case the free surface slope of the basic flow can be finite, but in the second case is small. The modulation equations are the local dispersion relation of the short waves, the kinematic equation for conservation of wave crests and the wave action equation. The results incorporate and extend the earlier work of Longuet-Higgins and Stewart [10, 11].

We study a periodic Kolmogorov model with m predators and n prey. By means of the comparison theorem and a Liapunov function, a set of easily verifiable sufficient conditions that guarantee the existence, uniqueness and global attractivity of the positive periodic solution is obtained. Finally, some suitable applications are given to illustrate that the conditions of the main theorem are feasible.

In this paper, we consider a class of combined optimal parameter selection and optimal control problems with general constraints. The first aim is to provide a unified approach to the numerical solution of this general class of optimisation problems by using the control parametrisation technique. This approach is supported by some convergence results. The second aim is to show that several different classes of optimal control problems can all be transformed into special cases of the problem considered in this paper. For illustration, four numerical examples are presented.

This paper is concerned with deformations corresponding to antiplane shear in finite elastostatics. The principal result is a necessary and sufficient condition for a homogeneous, isotropic, incompressible material to admit nontrivial states of anti-plane shear. The condition is given in terms of the strain energy density characteristic of the material and is illustrated by means of special examples.

In this paper we consider the asymptotics of extinction for the nonlinear diffusion reaction equation

with non-negative initial data possessing finite support. For t > 0, both solution and support vanish as t → T and x → x0. With T as the extinction time we construct the asymptotic solution as τ = T – t → 0 near the extinction point x0 using matched expansions. Taking x0= 0, we first form an outer expansion valid when η =xt–(m–p)/2 (1–p) = 0(1). This is nonuniformly valid for large |η| and has to be replaced by an intermediate expansion valid for |x| = O(τ−1/l0) where l0 is an even integer greater than unity. If p + m ≥ 2 this expansion is uniformly valid while for p + m < 2, there are regions near the edge of the support where diffusion becomes important. The zero order solution in these inner regions is discussed numerically.

The problem of determining a square integrable function from both its modulus and the modulus of its Fourier transform is studied. It is shown that for a large class of real functions the function is uniquely determined from this data. We also construct fundamental subsets of functions that are not uniquely determined. In quantum mechanical language, bound states are uniquely determined by their position and momentum distributions but, in general, scattering states are not.

This is an expository paper in which we present an introduction to a variational approach to spline interpolation. We present a sequence of theorems which starts with Holladay's classical result concerning natural cubic splines and culminates in some general abstract results.

The Schatten-von Neumann property of a pseudo-differential operator is established by showing that the pseudo-differential operator is a multiplier defined by means of an admissible wavelet associated to a unitary representation of the additive group Rn on the C*-algebra of all bounded linear operators from L2(Rn) into L2(Rn). A bounded linear operator on L2(R) arising in the Landau, Pollak and Slepian model in signal analysis is shown to be a wavelet multiplier studied in this paper.

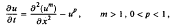
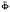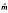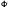
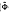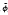
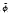
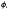
Given a pair of biorthogonal multiscaling functions, we present an algorithm for raising their approximation orders to any desired level. Precisely, let Φ(x) and (x) be a pair of biorthogonal multiscaling functions of multiplicity r, with approximation orders m and , respectively. Then for some integer 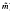s, we can construct a pair of new biorthogonal multiscaling functions Φnew(x) = [ΦT (x), φr+1 (x), φr+2(x),… φr+s(x)]T and new(x) = [ (x) T, r+1(x), r+2(x),… r+s(x)]T with approximation orders n (n > m) and ñ (ñ > ), respectively. In addition, corresponding to Φnew(x) and new(x) a biorthogonal multiwavelet pair ψnew(x) and new(x) is constructed explicitly. Finally, an example is given.