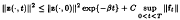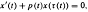Refine search
Actions for selected content:
8126 results in Fluid dynamics and solid mechanics
Usage of the convergence test of the residual norm in the Tsuno-Nodera version of the GMRES algorithm
-
- Journal:
- The ANZIAM Journal / Volume 49 / Issue 2 / October 2007
- Published online by Cambridge University Press:
- 17 February 2009, pp. 293-308
-
- Article
-
- You have access
- Export citation
Averaging of the Hamilton-Jacobi equation in infinite dimensions and an application
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 41 / Issue 3 / January 2000
- Published online by Cambridge University Press:
- 17 February 2009, pp. 372-385
-
- Article
-
- You have access
- Export citation
Numerical algorithms for constrained maximum likelihood estimation
-
- Journal:
- The ANZIAM Journal / Volume 45 / Issue 1 / July 2003
- Published online by Cambridge University Press:
- 17 February 2009, pp. 91-114
-
- Article
-
- You have access
- Export citation
An algorithm for solving the restricted least squares problem
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 21 / Issue 3 / January 1980
- Published online by Cambridge University Press:
- 17 February 2009, pp. 345-356
-
- Article
-
- You have access
- Export citation
Pointwise estimates for higher order convexity preserving polynomial approximation
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 36 / Issue 2 / October 1994
- Published online by Cambridge University Press:
- 17 February 2009, pp. 213-233
-
- Article
-
- You have access
- Export citation
A note on the boundary integral equation method for the solutions of second order elliptic equations
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 26 / Issue 4 / April 1985
- Published online by Cambridge University Press:
- 17 February 2009, pp. 415-421
-
- Article
-
- You have access
- Export citation
Some remarks on a quasi-steady-state approximation of the Navier-Stokes equation
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 29 / Issue 4 / April 1988
- Published online by Cambridge University Press:
- 17 February 2009, pp. 440-447
-
- Article
-
- You have access
- Export citation
On error bounds in strong approximations for eigenvalue problems
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 22 / Issue 3 / January 1981
- Published online by Cambridge University Press:
- 17 February 2009, pp. 270-283
-
- Article
-
- You have access
- Export citation
Oscillation of first-order delay differential equations
-
- Journal:
- The ANZIAM Journal / Volume 45 / Issue 4 / April 2004
- Published online by Cambridge University Press:
- 17 February 2009, pp. 593-599
-
- Article
-
- You have access
- Export citation
ANZ Volume 49 Issue 1 Cover and Front matter
-
- Journal:
- The ANZIAM Journal / Volume 49 / Issue 1 / July 2007
- Published online by Cambridge University Press:
- 17 February 2009, pp. f1-f4
-
- Article
-
- You have access
- Export citation
Inverse coefficient problems for nonlinear elliptic equations
-
- Journal:
- The ANZIAM Journal / Volume 49 / Issue 2 / October 2007
- Published online by Cambridge University Press:
- 17 February 2009, pp. 271-279
-
- Article
-
- You have access
- Export citation
ANZ volume 21 issue 2 Cover and Back matter
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 21 / Issue 2 / August 1979
- Published online by Cambridge University Press:
- 17 February 2009, pp. b1-b2
-
- Article
-
- You have access
- Export citation
Efficiency and generalised convexity in vector optimisation problems
-
- Journal:
- The ANZIAM Journal / Volume 45 / Issue 4 / April 2004
- Published online by Cambridge University Press:
- 17 February 2009, pp. 523-546
-
- Article
-
- You have access
- Export citation
Numerical solution of an evolution equation with a positive-type memory term
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 35 / Issue 1 / July 1993
- Published online by Cambridge University Press:
- 17 February 2009, pp. 23-70
-
- Article
-
- You have access
- Export citation
A programming problem with an Lp norm in the objective function
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 19 / Issue 3 / June 1976
- Published online by Cambridge University Press:
- 17 February 2009, pp. 333-342
-
- Article
-
- You have access
- Export citation
ANZ volume 47 issue 1 Cover and Back matter
-
- Journal:
- The ANZIAM Journal / Volume 47 / Issue 1 / July 2005
- Published online by Cambridge University Press:
- 17 February 2009, pp. b1-b3
-
- Article
-
- You have access
- Export citation
The anti-cyclonic shear wave: a new geophysical wave
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 25 / Issue 1 / July 1983
- Published online by Cambridge University Press:
- 17 February 2009, pp. 110-126
-
- Article
-
- You have access
- Export citation
Singular problems modelling phenomena in the theory of pseudoplastic fluids
-
- Journal:
- The ANZIAM Journal / Volume 45 / Issue 2 / October 2003
- Published online by Cambridge University Press:
- 17 February 2009, pp. 167-179
-
- Article
-
- You have access
- Export citation
Contents of Volume 27
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 27 / Issue 4 / April 1986
- Published online by Cambridge University Press:
- 17 February 2009, pp. 512-513
-
- Article
-
- You have access
- Export citation
Rank-1 perturbations and the Lanczos method, inverse iteration, and Krylov subspaces
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 36 / Issue 4 / April 1995
- Published online by Cambridge University Press:
- 17 February 2009, pp. 381-388
-
- Article
-
- You have access
- Export citation