Refine search
Actions for selected content:
8126 results in Fluid dynamics and solid mechanics
Inverse power law potentials about polygonal prisms and in polygonal cavities
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 20 / Issue 2 / December 1977
- Published online by Cambridge University Press:
- 17 February 2009, pp. 241-253
-
- Article
-
- You have access
- Export citation
A certain class of generating functions involving bilateral series
-
- Journal:
- The ANZIAM Journal / Volume 44 / Issue 3 / January 2003
- Published online by Cambridge University Press:
- 17 February 2009, pp. 475-483
-
- Article
-
- You have access
- Export citation
Explicit bounds for third-order difference equations
-
- Journal:
- The ANZIAM Journal / Volume 47 / Issue 3 / January 2006
- Published online by Cambridge University Press:
- 17 February 2009, pp. 359-366
-
- Article
-
- You have access
- Export citation
Dynamics of a delayed population model with feedback control
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 41 / Issue 4 / April 2000
- Published online by Cambridge University Press:
- 17 February 2009, pp. 451-457
-
- Article
-
- You have access
- Export citation
ANZ volume 19 issue 4 Cover and Back matter
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 19 / Issue 4 / December 1976
- Published online by Cambridge University Press:
- 17 February 2009, pp. b1-b2
-
- Article
-
- You have access
- Export citation
A three-dimensional numerical model of the response of the Australian North West Shelf to tropical cyclones
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 36 / Issue 1 / July 1994
- Published online by Cambridge University Press:
- 17 February 2009, pp. 64-100
-
- Article
-
- You have access
- Export citation
Collocation methods for two dimensional weakly singular integral equations
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 22 / Issue 4 / April 1981
- Published online by Cambridge University Press:
- 17 February 2009, pp. 456-473
-
- Article
-
- You have access
- Export citation
ANZ volume 39 issue 2 Cover and Back matter
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 39 / Issue 2 / October 1997
- Published online by Cambridge University Press:
- 17 February 2009, pp. b1-b2
-
- Article
-
- You have access
- Export citation
A C0-Collocation-like method for elliptic equations on rectangular regions
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 38 / Issue 3 / January 1997
- Published online by Cambridge University Press:
- 17 February 2009, pp. 368-387
-
- Article
-
- You have access
- Export citation
Concise representation of generalised gradients
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 28 / Issue 1 / July 1986
- Published online by Cambridge University Press:
- 17 February 2009, pp. 57-74
-
- Article
-
- You have access
- Export citation
Infinitely divisible random transition probabilities with application to dependent Markov chains
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 25 / Issue 4 / April 1984
- Published online by Cambridge University Press:
- 17 February 2009, pp. 463-472
-
- Article
-
- You have access
- Export citation
ANZ volume 41 issue 4 Cover and Back matter
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 41 / Issue 4 / April 2000
- Published online by Cambridge University Press:
- 17 February 2009, pp. b1-b2
-
- Article
-
- You have access
- Export citation
The effect of an enclosed air cavity on a rectangular drum
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 24 / Issue 3 / January 1983
- Published online by Cambridge University Press:
- 17 February 2009, pp. 343-349
-
- Article
-
- You have access
- Export citation
Continuous-time quadratic cost flow problems with applications to water distribution networks
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 37 / Issue 4 / April 1996
- Published online by Cambridge University Press:
- 17 February 2009, pp. 530-548
-
- Article
-
- You have access
- Export citation
ANZ volume 42 issue 2 Cover and Front matter
-
- Journal:
- The ANZIAM Journal / Volume 42 / Issue 2 / October 2000
- Published online by Cambridge University Press:
- 17 February 2009, pp. f1-f4
-
- Article
-
- You have access
- Export citation
Some boundary-value problems for nonlinear (N) diffusion and pseudo-plastic flow
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 33 / Issue 3 / January 1992
- Published online by Cambridge University Press:
- 17 February 2009, pp. 255-268
-
- Article
-
- You have access
- Export citation
On the solution of a structured nonlinear programme
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 19 / Issue 2 / December 1975
- Published online by Cambridge University Press:
- 17 February 2009, pp. 242-248
-
- Article
-
- You have access
- Export citation
On hearing the shape of an arbitrary doubly-connected region in R2
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 31 / Issue 4 / April 1990
- Published online by Cambridge University Press:
- 17 February 2009, pp. 472-483
-
- Article
-
- You have access
- Export citation
Discrete Liapunov functions with Δ2V>0
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 20 / Issue 3 / June 1978
- Published online by Cambridge University Press:
- 17 February 2009, pp. 280-284
-
- Article
-
- You have access
- Export citation
A formal comparison of methods proposed for the numerical solution of first kind integral equations
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 22 / Issue 4 / April 1981
- Published online by Cambridge University Press:
- 17 February 2009, pp. 488-500
-
- Article
-
- You have access
- Export citation
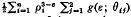 . Here ρ
. Here ρ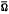 ⊆
⊆ 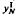 and
and 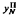 , two different numerical approximations to its solution, using the collocation and iterated collocation methods respectively. We describe without proof some known results concerning the general convergence properties of
, two different numerical approximations to its solution, using the collocation and iterated collocation methods respectively. We describe without proof some known results concerning the general convergence properties of 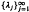 for the two-dimensional Laplacian using the asymptotic expansion of the spectral function
for the two-dimensional Laplacian using the asymptotic expansion of the spectral function 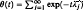 for small positive
for small positive 