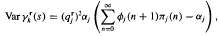Refine search
Actions for selected content:
8126 results in Fluid dynamics and solid mechanics
Global stability and persistence in diffusive food chains
-
- Journal:
- The ANZIAM Journal / Volume 43 / Issue 2 / October 2001
- Published online by Cambridge University Press:
- 17 February 2009, pp. 247-268
-
- Article
-
- You have access
- Export citation
Homotopy continuation method for the numerical solutions of generalised symmetric eigenvalue problems
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 32 / Issue 4 / April 1991
- Published online by Cambridge University Press:
- 17 February 2009, pp. 437-456
-
- Article
-
- You have access
- Export citation
Some Bianchi type VI0 viscous fluid cosmological models
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 33 / Issue 1 / July 1991
- Published online by Cambridge University Press:
- 17 February 2009, pp. 77-84
-
- Article
-
- You have access
- Export citation
A note on the small-time development of the solution to a coupled, nonlinear, singular reaction-diffusion system
-
- Journal:
- The ANZIAM Journal / Volume 47 / Issue 4 / April 2006
- Published online by Cambridge University Press:
- 17 February 2009, pp. 581-591
-
- Article
-
- You have access
- Export citation
A note on the convergence of Halley's method for solving operator equations
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 37 / Issue 1 / July 1995
- Published online by Cambridge University Press:
- 17 February 2009, pp. 16-25
-
- Article
-
- You have access
- Export citation
Reduction of second order linear dynamical systems, with large dissipation, by state variable transformations
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 32 / Issue 2 / October 1990
- Published online by Cambridge University Press:
- 17 February 2009, pp. 207-222
-
- Article
-
- You have access
- Export citation
An affine scaling interior point backtracking algorithm for nonlinear constrained optimisation
-
- Journal:
- The ANZIAM Journal / Volume 46 / Issue 1 / July 2004
- Published online by Cambridge University Press:
- 17 February 2009, pp. 45-66
-
- Article
-
- You have access
- Export citation
Wavelet and discrete cosine transforms for inserting information into BMP images
-
- Journal:
- The ANZIAM Journal / Volume 48 / Issue 1 / July 2006
- Published online by Cambridge University Press:
- 17 February 2009, pp. 23-35
-
- Article
-
- You have access
- Export citation
Sparse matrix factorizations of transfer matrices
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 28 / Issue 4 / April 1987
- Published online by Cambridge University Press:
- 17 February 2009, pp. 462-475
-
- Article
-
- You have access
- Export citation
Bilinear and bilateral generating functions of generalized polynomials
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 39 / Issue 2 / October 1997
- Published online by Cambridge University Press:
- 17 February 2009, pp. 257-270
-
- Article
-
- You have access
- Export citation
Poisson approximations for telecommunications networks
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 36 / Issue 1 / July 1994
- Published online by Cambridge University Press:
- 17 February 2009, p. 132
-
- Article
-
- You have access
- Export citation
A cusp-like free-surface flow due to a submerged source or sink
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 25 / Issue 4 / April 1984
- Published online by Cambridge University Press:
- 17 February 2009, pp. 443-450
-
- Article
-
- You have access
- Export citation
Love's integral and other relations between solutions to mixed boundary-value problems in potential theory
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 22 / Issue 3 / January 1981
- Published online by Cambridge University Press:
- 17 February 2009, pp. 353-367
-
- Article
-
- You have access
- Export citation
Strong uniqueness in sequential linear programming
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 31 / Issue 4 / April 1990
- Published online by Cambridge University Press:
- 17 February 2009, pp. 379-384
-
- Article
-
- You have access
- Export citation
ANZ volume 36 issue 1 Cover and Back matter
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 36 / Issue 1 / July 1994
- Published online by Cambridge University Press:
- 17 February 2009, pp. b1-b2
-
- Article
-
- You have access
- Export citation
ANZ volume 31 issue 3 Cover and Back matter
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 31 / Issue 3 / January 1990
- Published online by Cambridge University Press:
- 17 February 2009, pp. b1-b2
-
- Article
-
- You have access
- Export citation
Extreme stability and almost periodicity in continuous and discrete neuronal models with finite delays
-
- Journal:
- The ANZIAM Journal / Volume 44 / Issue 2 / October 2002
- Published online by Cambridge University Press:
- 17 February 2009, pp. 261-282
-
- Article
-
- You have access
- Export citation
ANZ volume 20 issue 3 Cover and Back matter
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 20 / Issue 3 / June 1978
- Published online by Cambridge University Press:
- 17 February 2009, pp. b1-b2
-
- Article
-
- You have access
- Export citation
Static plane-symmetric solution of a scalar-tensor theory of gravitation
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 24 / Issue 3 / January 1983
- Published online by Cambridge University Press:
- 17 February 2009, pp. 339-342
-
- Article
-
- You have access
- Export citation
Initial value formalism for Lemaitre-Tolman-Bondi collapse
-
- Journal:
- The ANZIAM Journal / Volume 49 / Issue 1 / July 2007
- Published online by Cambridge University Press:
- 17 February 2009, pp. 53-73
-
- Article
-
- You have access
- Export citation
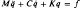 are transformed by linear state variable transformations
are transformed by linear state variable transformations 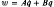 , where
, where