Refine search
Actions for selected content:
8126 results in Fluid dynamics and solid mechanics
Minimal and maximal solutions to systems of differential equations with a singular matrix
-
- Journal:
- The ANZIAM Journal / Volume 45 / Issue 2 / October 2003
- Published online by Cambridge University Press:
- 17 February 2009, pp. 223-231
-
- Article
-
- You have access
- Export citation
ANZ volume 32 issue 3 Cover and Back matter
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 32 / Issue 3 / January 1991
- Published online by Cambridge University Press:
- 17 February 2009, pp. b1-b2
-
- Article
-
- You have access
- Export citation
On a complementarity problem associated with nondifferentiable programming
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 25 / Issue 3 / January 1984
- Published online by Cambridge University Press:
- 17 February 2009, pp. 419-430
-
- Article
-
- You have access
- Export citation
ANZ volume 28 issue 3 Cover and Back matter
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 28 / Issue 3 / January 1987
- Published online by Cambridge University Press:
- 17 February 2009, pp. b1-b2
-
- Article
-
- You have access
- Export citation
Asymptotic behaviour of second-order difference equations
-
- Journal:
- The ANZIAM Journal / Volume 46 / Issue 1 / July 2004
- Published online by Cambridge University Press:
- 17 February 2009, pp. 157-170
-
- Article
-
- You have access
- Export citation
The exponential of a constant matrix on time scales
-
- Journal:
- The ANZIAM Journal / Volume 48 / Issue 1 / July 2006
- Published online by Cambridge University Press:
- 17 February 2009, pp. 99-106
-
- Article
-
- You have access
- Export citation
The lumped mass finite element method for a parabolic problem
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 26 / Issue 3 / January 1985
- Published online by Cambridge University Press:
- 17 February 2009, pp. 329-354
-
- Article
-
- You have access
- Export citation
Waves below first cutoff in a duct
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 29 / Issue 4 / April 1988
- Published online by Cambridge University Press:
- 17 February 2009, pp. 448-460
-
- Article
-
- You have access
- Export citation
The effect of viscous dissipation on non-linear convection at high Rayleigh number
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 19 / Issue 2 / December 1975
- Published online by Cambridge University Press:
- 17 February 2009, pp. 165-172
-
- Article
-
- You have access
- Export citation
A gradient technique for an optimal control problem governed by a system of nonlinear first order partial differential equations
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 36 / Issue 3 / January 1995
- Published online by Cambridge University Press:
- 17 February 2009, pp. 261-273
-
- Article
-
- You have access
- Export citation
The “global” convergence of Broyden-like methods with suitable line search
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 28 / Issue 1 / July 1986
- Published online by Cambridge University Press:
- 17 February 2009, pp. 75-92
-
- Article
-
- You have access
- Export citation
A characterisation of Newton maps
-
- Journal:
- The ANZIAM Journal / Volume 48 / Issue 2 / October 2006
- Published online by Cambridge University Press:
- 17 February 2009, pp. 211-223
-
- Article
-
- You have access
- Export citation
On a distribution of Leipnik and Pearce
-
- Journal:
- The ANZIAM Journal / Volume 48 / Issue 3 / January 2007
- Published online by Cambridge University Press:
- 17 February 2009, pp. 405-407
-
- Article
-
- You have access
- Export citation
Effects of iron on a toroidal conductor
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 23 / Issue 1 / July 1981
- Published online by Cambridge University Press:
- 17 February 2009, pp. 103-114
-
- Article
-
- You have access
- Export citation
ANZ volume 33 issue 2 Cover and Front matter
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 33 / Issue 2 / October 1991
- Published online by Cambridge University Press:
- 17 February 2009, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Axisymmertic Stokes flow images in spherical free surfaces with applications to rising bubbles
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 25 / Issue 2 / October 1983
- Published online by Cambridge University Press:
- 17 February 2009, pp. 217-231
-
- Article
-
- You have access
- Export citation
The characteristic identities and reduced matrix elements of the unitary and orthogonal groups
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 20 / Issue 4 / December 1978
- Published online by Cambridge University Press:
- 17 February 2009, pp. 401-433
-
- Article
-
- You have access
- Export citation
On the Cauchy problem for the 1+2 complex Ginzburg-Landau equation
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 36 / Issue 3 / January 1995
- Published online by Cambridge University Press:
- 17 February 2009, pp. 313-324
-
- Article
-
- You have access
- Export citation
ANZ volume 28 issue 4 Cover and Back matter
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 28 / Issue 4 / April 1987
- Published online by Cambridge University Press:
- 17 February 2009, pp. b1-b2
-
- Article
-
- You have access
- Export citation
On tensor operators and characteristic identities for semi-simple Lie algebras
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 20 / Issue 3 / June 1978
- Published online by Cambridge University Press:
- 17 February 2009, pp. 290-314
-
- Article
-
- You have access
- Export citation
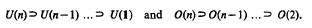
 .
.