Refine search
Actions for selected content:
8126 results in Fluid dynamics and solid mechanics
On an extension of generalized incomplete Gamma functions with applications
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 37 / Issue 3 / January 1996
- Published online by Cambridge University Press:
- 17 February 2009, pp. 392-405
-
- Article
-
- You have access
- Export citation
Solutions of period four for a non-linear difference equation
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 26 / Issue 2 / October 1984
- Published online by Cambridge University Press:
- 17 February 2009, pp. 146-164
-
- Article
-
- You have access
- Export citation
An application of Newton's method to differential and integral equations
-
- Journal:
- The ANZIAM Journal / Volume 42 / Issue 3 / January 2001
- Published online by Cambridge University Press:
- 17 February 2009, pp. 372-386
-
- Article
-
- You have access
- Export citation
On the unsteady squeezing of a viscous fluid from a tube
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 21 / Issue 1 / April 1979
- Published online by Cambridge University Press:
- 17 February 2009, pp. 65-74
-
- Article
-
- You have access
- Export citation
Nonlinear electron solutions and their characteristics at infinity
-
- Journal:
- The ANZIAM Journal / Volume 44 / Issue 1 / July 2002
- Published online by Cambridge University Press:
- 17 February 2009, pp. 51-59
-
- Article
-
- You have access
- Export citation
ANZ volume 45 issue 2 Cover and Front matter
-
- Journal:
- The ANZIAM Journal / Volume 45 / Issue 2 / October 2003
- Published online by Cambridge University Press:
- 17 February 2009, pp. f1-f4
-
- Article
-
- You have access
- Export citation
Internal solitary waves with stratification in density
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 38 / Issue 4 / April 1997
- Published online by Cambridge University Press:
- 17 February 2009, pp. 563-580
-
- Article
-
- You have access
- Export citation
Equilibrium states of a Bose gas with repulsive interactions
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 22 / Issue 2 / October 1980
- Published online by Cambridge University Press:
- 17 February 2009, pp. 129-147
-
- Article
-
- You have access
- Export citation
On the explosion of chain-thermal reactions
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 24 / Issue 2 / October 1982
- Published online by Cambridge University Press:
- 17 February 2009, pp. 194-202
-
- Article
-
- You have access
- Export citation
Cost-time trade-off in three-axial sums' transportation problem
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 35 / Issue 4 / April 1994
- Published online by Cambridge University Press:
- 17 February 2009, pp. 498-505
-
- Article
-
- You have access
- Export citation
A comparison of constraint qualifications in infinite-dimensional convex programming revisited
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 40 / Issue 3 / January 1999
- Published online by Cambridge University Press:
- 17 February 2009, pp. 353-378
-
- Article
-
- You have access
- Export citation
Strong system equivalence (II)
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 27 / Issue 2 / October 1985
- Published online by Cambridge University Press:
- 17 February 2009, pp. 223-237
-
- Article
-
- You have access
- Export citation
Criticality dependence on data and parameters for a problem in combustion theory, with temperature-dependent conductivity
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 31 / Issue 1 / July 1989
- Published online by Cambridge University Press:
- 17 February 2009, pp. 76-80
-
- Article
-
- You have access
- Export citation
Solution of a general liner difference equation
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 22 / Issue 3 / January 1981
- Published online by Cambridge University Press:
- 17 February 2009, pp. 314-317
-
- Article
-
- You have access
- Export citation
Saddle point and duality in the optimization theory of convex set functions
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 24 / Issue 2 / October 1982
- Published online by Cambridge University Press:
- 17 February 2009, pp. 130-137
-
- Article
-
- You have access
- Export citation
ANZ volume 43 issue 2 Cover and Front matter
-
- Journal:
- The ANZIAM Journal / Volume 43 / Issue 2 / October 2001
- Published online by Cambridge University Press:
- 17 February 2009, pp. f1-f4
-
- Article
-
- You have access
- Export citation
Numerical integration of the axisymmetric Robinson-Trautman equation by a spectral method
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 41 / Issue 2 / October 1999
- Published online by Cambridge University Press:
- 17 February 2009, pp. 271-280
-
- Article
-
- You have access
- Export citation
A bioeconomic model of nonselective harvesting of two competing fish species
-
- Journal:
- The ANZIAM Journal / Volume 46 / Issue 2 / October 2004
- Published online by Cambridge University Press:
- 17 February 2009, pp. 299-308
-
- Article
-
- You have access
- Export citation
The iterated projection solution for the Fredholm integral equation of second kind
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 22 / Issue 4 / April 1981
- Published online by Cambridge University Press:
- 17 February 2009, pp. 439-451
-
- Article
-
- You have access
- Export citation
Deferred correction for the integral equation eigenvalue problem
-
- Journal:
- Journal of the Australian Mathematical Society. Series B. Applied Mathematics / Volume 22 / Issue 4 / April 1981
- Published online by Cambridge University Press:
- 17 February 2009, pp. 474-487
-
- Article
-
- You have access
- Export citation
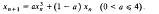
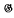 ,
, 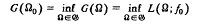
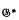 (for the definition, see the later context).
(for the definition, see the later context).