This note examines maximum principles for systems of parabolic partial differential equations describing diffusion in the presence of three diffusion paths. The particular system under consideration arises from a random walk model. For a more general system constraints on the various constants are given which guarantee maximum principles. Remarkably, the physical system arising from the random walk model automatically satisfies these constraints.

A method for determining the upper and lower bounds for performance measures for certain types of Generalised Semi-Markov Processes has been described in Taylor and Coyle [8]. A brief description of this method and its use in finding an upper bound for the time congestion of a GI/M/n/n queueing system will be given. This bound turns out to have a simple form which is quickly calculated and easy to use in practice.

In an earlier paper [4], the author showed how Laplace transforms might be assigned to a class of superexponential functions for which the usual defining integral diverges. The present paper considers the case of the function exp(et), which arises in combinatorial contexts and whose Laplace transform may be assigned by means of an extension of techniques described in the previous paper.

We discuss the separability of the Hamilton-Jacobi equation for the Kerr metric. We use a recent theorem which says that a completely integrable geodesic equation has a fully separable Hamilton-Jacobi equation if and only if the Lagrangian is a composite of the involutive first integrals. We also discuss the physical significance of Carter's fourth constant in terms of the symplectic reduction of the Schwarzschild metric via SO(3), showing that the Killing tensor quantity is the remnant of the square of angular momentum.

It is shown that the necessary and sufficient condition for the transposition invariance of the field equations derivable from an Einstein-Kaufman variational action principle is the vanishing of xythe vector Γλ. When this condition is satisfied, the field equations become the so-called strong field equations of Einstein. In this sense, the latter can be claimed to follow from the same action principle.

In this paper, we study Pontryagin's maximum principle for some optimal control problems governed by a non-well-posed parabolic differential equation. A new penalty functional is applied to derive Pontryagin's maximum principle and an application for this system is given.

The decay at large wavenumbers of the energy density in an inertial wave generated in a sphere by an arbitrary initial disturbance is determined as a first step to a comparison with the general theory of Phillips [17] for a statistically steady field of random inertial waves in an arbitrary cavity.

The authors consider the higher-order nonlinear neutral delay difference equation

and obtain results on the asymptotic behavior of solutions when (pn) is allowed to oscillate about the bifurcation value –1. We also consider the case where the sequence {pn} has arbitrarily large zeros. Examples illustrating the results are included, and suggestions for further research are indicated.

We study the discrete asymptotic stability conditions of the perturbed system of first-order linear difference equations with periodic coefficients under the assumption that the related unperturbed system is discrete asymptotically stable. These conditions are dependent on the perturbation matrix B(n) itself and a different parameter is given for obtaining some estimates for the solutions of the unperturbed system.

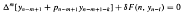
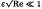The evolution of the critical layer in a viscous, stratified fluid is examined in the limit of large Richardson and Reynolds numbers. A source far above the critical layer and of amplitude ɛ is turned on at t = 0 and the behaviour of both the steady state and transients is found. Viscosity dominates over nonlinearity in the critical layer for , Re being an appropriately defined Reynolds number. Wave amplitudes are found to grow as the critical layer is approached, then decay rapidly due to the action of viscosity in a critical layer of O((Re)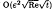−1/3) around the critical level. The critical layer acts as a source of vorticity, which diffuses into the outer flow, resulting in an induced mean flow of . This induced mean flow causes the critical level to move towards the incoming wave.

The unsteady Hele-Shaw problem is a model nonlinear system that, for a certain parameter ranger, exhibits the phenomenon known as viscous fingering. While not directly applicable to multiphase porous-media flow, it does prove to be an adequate mathematical model for unstable dieplacement in laboratory parallel-plate devices. We seek here to determine, by use of an accurate boundary-integral frount-tracking scheme, the extent to which the simplified system captures the canonical nonlinear behavior of displacement flows and, in particular, to ascertain the role of noise in such systems. We choose to study a particular pattern of injection and production “wells.” The pattern chosen is the isolated “five-spot,” that is a single source surrounded by four symmetrically-placed sinks in an infinite two-dimensional “reservoir.” In cases where the “pusher” fluid has negligible viscosity, sweep efficiency is calculated for a range of values of the single dimensionless parameter τ, an inverse capillary number. As this parameter is reduced, corresponding to increased flow rate or reduced interfacial tension, this efficiency decreases continuously. For small values of τ, these stable displacements change abruptly to a regime characterized by unstable competing fingers and a significant reduction in sweep efficiency. A simple stability argument appears to correctly predict the noise level required to transit from the stable to the competing-finger regimes. Published compilations of experimental results for sweep efficiency as a function of viscosity ratio showed an unexplained divergence when the pusher fluid is less viscous. Our simulations produce a similar divergence when, for a given viscosity ratio, the parameter τ is varied.

We are concerned with the existence of solutions of

where Δp is the p-Laplacian, p ∈ (1, ∞), and Ω is a bounded smooth domain in ℝn.

For h(x) ≡ 0 and f(x, u) satisfying proper asymptotic spectral conditions, existence of a unique positive solution is obtained by invoking the sub-supersolution technique and the spectral method. For h(x) ≢ 0, with assumptions on asymptotic behavior of f(x, u) as u → ±∞, an existence result is also proved.

In this paper we derive extremality and comparison results for explicit and implicit initial and boundary value problems of first-order differential equations. Both the differential equations and the boundary conditions may involve discontinuities.