Coplanar forced oscillations of a mechanical system such as a seismometer or a fluid in a tank are modelled by the coplanar motion of periodically forced, weakly damped pendulum. We consider the phase-locked solutions of the differential equation governing planar motion of a weakly damped pendulum driven by a periodic torque. Sinusoidal approximations previously obtained for downward and inverted oscillations at small values of the dimensionless driving amplitude ε are continued into numerical solutions at larger values of ε. Resonance curves and stability boundaries are presented for downward and inverted oscillations of periods T, 2T, and 4T, where T(≡ 2π/ω) is the dimensionless forcing period. The symmetry-breaking, period-doubling sequences of oscillatory motion are found to occur in bands on the (ω, ε) plane, with the amplitudes of stable oscillations in one band differing by multiples of about π from those in the other bands, a structure similar to that of energy levels in wave mechanics. The sinusoidal approximations for symmetric T-periodic oscillations prove to be surprisingly accurate at the larger values of ε, the banded structure being related to the periodicity of the J0 Bessel function.

Equations are derived to approximately describe the propagation of small amplitude surface and interfacial waves across small irregularities in depth in a two-layer fluid. When the irregularities are sinusoidal, Bragg interaction effects between an incident surface wave and the bottom corrugations can lead to a large-amplitude reflected interfacial wave or a large-amplitude transmitted interfacial wave if the incident surface wave is relatively long and the lower layer shallow in comparison with the upper layer.

We solve the problem of finding a simultaneous matrix normal form for an element of the Lie algebra o(p, q) and the underlying indefinite inner product. The results are used to determine several classes of classical Hamiltonian dynamical systems which possess a first integral linear in the momentum variables.

An integral involving a combination of Legendre polynomials, exponential and algebraic terms is solved using the generating function. Special cases of this result are compared with known expansions, and the previously known results are shown to be extendible to a particularly pleasing result as a limiting case. Comparisons provide some new combinatorial identities involving binomials. Finally, an effective numerical procedure is described which evaluates the integral to machine accuracy.

The problem of heat transfer in a duct or tube for large values of the Péclet number has traditionally been solved by assuming that diffusion in the axial direction is negligible. This approach was used by Graetz [2] for the circular tube and by Prins et al [5] for the flat duct to obtain a series solution for downstream temperature field.

Since these series converge very slowly in the neighbourhood of the origin, some other approach is necessary in the thermal entrance region. This was supplied by Lévêque [3] and extended by Mercer [4] who matched the Lévêque solution to the eigenfunction expansion.

In all these solutions it was assumed that the axial diffusion of heat was negligible, but this assumption is invalid close to the discontinuity, since in this region the axial temperature gradient is large and the fluid velocity is small, so that axial diffusion plays an important role.

In this paper, the assumptions implicit in Lévêque's solution are re-examined, and the correct approximation in the neighbourhood of the discontinuity as well as the solution which matches this into Lévêque's solution are presented. In the first of these solutions, diffusion is the only heat-transfer mechanism, while in the matching solution diffusion and convection are in balance.

The corresponding solutions for the case of prescribed flux on the boundary are also considered.

A numerical procedure for calculating the evolution of a periodic interface between two immiscible fluids flowing in a two-dimensional porous medium or Hele-Shaw cell is described. The motion of the interface is determined in a stepwise manner with its new velocity at exach time step being derived as a numerical solution of a boundary integral equation. Attention is focused on the case of unstable displacement charaterised physically by the “fingering” of the interface and computationally by the growth of numerical errors regardless of the numerical method employed. Here the growth of such error is reduced and the usable part of the calculation extended to finite amplitudes. Numerical results are compared with an exact “finger” solution and the calculated behaviour of an initial sinusoidal displacement, as a function of interfacial tension, initial amplitude and wavelength, is discussed.

The steady-state heating of a two-dimensional slab by the TE10 mode in a microwave cavity is considered. The cavity contains an iris with a variable aperture and is closed by a short. Resonance can occur in the cavity, which is dependent on the short position, the aperture width and the temperature of the heated slab.

The governing equations for the slab are steady-state versions of the forced heat equation and Maxwell's equations while fixed-temperature boundary conditions are used. An Arrhenius temperature dependency is assumed for both the electrical conductivity and the thermal absorptivity. Semi-analytical solutions, valid for small thermal absorptivity, are found for the steady-state temperature and the electric-field amplitude in the slab using the Galerkin method.

With no-iris (a semi-infinite waveguide) the usual S-shaped power versus temperature curve occurs. As the aperture width is varied however, the critical power level at which thermal runaway occurs and the temperature response on the upper branch of the S-shaped curve are both changed. This is due to the interaction between the radiation, the cavity and the heated slab. An example is presented to illustrate these aperture effects. Also, it is shown that an optimal aperture setting and short position exists which minimises the input power needed to obtain a given temperature.

We continue our study of the adaptation from spherical to doubly periodic slot domains of the poloidal-toroidal representation of vector fields. Building on the successful construction of an orthogonal quinquepartite decomposition of doubly periodic vector fields of arbitrary divergence with integral representations for the projections of known vector fields and equivalent scalar representations for unknown vector fields (Part 1), we now present a decomposition of vector field equations into an equivalent set of scalar field equations. The Stokes equations for slow viscous incompressible fluid flow in an arbitrary force field are treated as an example, and for them the application of the decomposition uncouples the conservation of momentum equation from the conservation of mass constraint. The resulting scalar equations are then solved by elementary methods. The extension to generalised Stokes equations resulting from the application of various time discretisation schemes to the Navier-Stokes equations is also solved.

Integral equations on the half line are commonly approximated by the finite-section approximation, in which the infinite upper limit is replaced by a positive number β. A novel technique is used here to rederive a number of classical results on the existence and uniqueness of the solution of the Wiener-Hopf and related equations, and is then extended to obtain existence, uniqueness and convergence results for the corresponding finite-section equations. Unlike the methods used in the recent work of Anselone and Sloan, the present methods are constructive, and result in explicit asymptotic bounds for the error introduced by the finite-section approximation.

The new motion of embedding a centre manifold in some higher-dimensional manifold leads to a practical approach to the rational low-dimensional approximation of a wide class of dynamical systems; it also provides a simple geometric picture for these approximations. In particular, I consider the problem of finding an approximate, but accurate, description of the evolution of a two-dimensional planform of convection. Inspired by a simple example, the straightforward adiabatic iteration is proposed to estimate an embedding manifold and arguments are presented for its effectiveness. Upon applying the procedure to a model convective planform problem I find that the resulting approximations perform remarkably well–much better than the traditional Swift-Hohenberg approximation for planform evolution.

A population of cells growing and dividing often goes through a phase of exponential growth of numbers, during which the size distribution remains steady. In this paper we study the function differential equation governing this steady size distribution in the particular case where the individual cells themselves are growing exponentially in size. A series solution is obtained for the case where the probability of cell division is proportional to any positive power of the cell size, and a method for finding closed-form solutions for a more general class of cell division functions is developed.

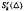Let Δ denote a triangulation of a planar polygon Ω. For any positive integer 0 ≤ r < k, let denote the vector space of functions in 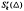Cr whose restrictions to each triangle of Δ are polynomials of total degree at most k. Such spaces, called bivariate spline spaces, have many applications in surface fitting, scattered data interpolation, function approximation and numerical solutions of partial differential equations. An important problem is to give the function expression. In this paper, we prove that, if (Δ, Ω) is type-X, then any bivariate spline function in can be expressed by a series of univariate polynomials and a special bivariate finite element function in 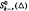satisfying a so-called integral conformality condition system. We also give a direct sum decomposition of the space 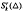. In addition, the dimension of 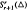for a kind of triangulation has been determined.

The problem of an infinitely long rigid punch of uniform cross-section moving across a viscoelastic half-space at constant velocity, large enough so that inertial effects cannot be neglected, is examined and solved in various approximations. Frictional shear is assumed to exist between the punch and the half-space. The method, which is an extension of that developed in previous papers [6, 7], is applicable for any form of viscoelastic behaviour in the half-space. For the special case of discrete spectrum behaviour the method is described in detail. For the case where the punch is cylindrical and viscoelastic effects are small compared with elastic effects, explicit expressions are given for all quantities of interest, in particular the coefficient of hysteretic friction. A general Hilbert transform formula is derived in the appendix.

A two component classical Coulomb system is considered, in which particles of charge +q and + 2q are constrained to lie on a circle and interact via the two-dimensional Coulomb potential. At a special value of the coupling constant the correlation functions are calculated exactly and the asymptotic form of the truncated charge-charge correlation is found to obey Jancovici's sum rule.