A parallel algorithm is developed for the numerical solution of the diffusion equation ut = uxx, 0 < x < t < T, subject to u(x, 0) = f(x), ux(X, t) = g(t) and the specification of mass .

We consider an age-structured population model achieved by modifying the classical Sharpe-Lotka-McKendrick model, incorporating an overcrowding effect or competition for resources term. This term depends on the whole population rather than on any specific age group, in the case of overcrowding or limitation of resources. We investigate the solutions for arbitrary initial conditions. We consider the existence of a steady age distribution and its stability and are able to determine this for a simple illustrative case. If the non-trivial steady age distribution is unstable, there is a critical initial population size beyond which the population explodes. This watershed is independent of the shape of the initial age distribution.

A collocation method for Symm's integral equation on an interval (a first-kind integral equation with logarithmic kernel), in which the basis functions are Chebyshev polynomials multiplied by an appropriate singular function and the collocation points are Chebyshev points, is analysed. The novel feature lies in the analysis, which introduces Sobolev norms that respect the singularity structure of the exact solution at the ends of the interval. The rate of convergence is shown to be faster than any negative power of n, the degree of the polynomial space, if the driving term is smooth.

The following figure has been reprinted since the one on page 30 of the previous issue (ANZIAM J. vol. 48 part 1) is unsatisfactory.

A simple and efficient numerical technique for the buckling analysis of thin elastic plates of arbitrary shape is proposed. The approach is based upon the combination of the standard Finite Element Method with the constant deflection contour method. Several representative plate problems of irregular boundaries are treated and where possible, the obtained results are validated against corresponding results in the literature.

Taylor's model of dispersion simply describes the long-term spread of material along a pipe, channel or river. However, often we need multi-mode models to resolve finer details in space and time. Here we construct zonal models of dispersion via the new principle of matching their long-term evolution with that of the original problem. Using centre manifold techniques this is done straightforwardly and systematically. Furthermore, this approach provides correct initial and boundary conditions for the zonal models. We expect the proposed principle of matched centre manifold evolution to be useful in a wide range of modelling problems.

The qualitative behavior of positive solutions of the neutral-delay two-species Lotka-Volterra competitive system with several discrete delays is investigated. Sufficient conditions are obtained for the local asymptotic stability of the positive steady state. In fact, some of these sufficient conditions are also necessary except at those critical values. Results on the oscillatory and non-oscillatory characteristics of the positive solutions are also included.

Instantaneous streamlines, particle pathlines and pressure contours for a cavitation bubble in the vicinity of a free surface and near a rigid boundary are obtained. During the collapse phase of a bubble near a free surface, the streamlines show the existence of a stagnation point between the bubble and the free surface which occurs at a different location from the point of maximum pressure. This phenomenon exists when the initial distance of the bubble is sufficiently close to the free surface for the bubble and free surface to move in opposite directions during collapse of the bubble. Pressure calculations during the collapse of a cavitation bubble near a rigid boundary show that the maximum pressure is substantially larger than the equivalent Rayleigh bubble of the same volume.

Steady two-dimensional flows in a domain bounded below by an infinite horizontal wall and above by a semi-infinite horizontal wall, a vertical wall and a free surface are considered. The fluid is assumed to be inviscid and incompressible, and gravity is taken into account. The problem is solved numerically by series truncation. It is shown that for a given length of the vertical wall, there are two families of solutions. One family is characterized by a continuous slope at the separation point and a limiting configuration with a stagnation point and a 120° angle corner at the separation point. The other family is characterized by a stagnation point and a 90° angle corner at the separation point. Flows under a sluice gate with and without a rigid lid approximation upstream are also considered.

The contact problem investigated in this paper may be more fully described as a three dimensional elastic body with a circular hole through it; inside this tunnel is press fitted a solid elastic plug of finite length. Shear stresses are taken to be absent along the contact interface.

An influence coefficient technique is used to model the governing integral equation. For the elastic region the displacement influence coefficients due to bands of constant pressure are determined using a numerical quadrature on Fourier integrals. However, the plug, being of finite length, requires the superposition of two separate solutions to boundary value problems before the displacement influence coefficients can be determined.

Contact pressure distributions are presented for a sample of parameter variations and also for a case where hydrostatic pressure is present in the tunnel in the elastic region. Despite both components being elastic the imposition of a constant interference displacement along the interface still gives rise to the characteristic singularity in contact pressure at the edges of contact due to the strain discontinuity at these points.

Elastic behaviour of a nonhomogeneous transversely isotropic half-space is studied under the action of a smooth rigid axisymmetric indentor. Hankel transforms of different orders have been used. It is observed that in contrast to a homogeneous medium, the pressure distribution in the contact region in a nonhomogeneous medium is not directly available, rather it is obtainable from the solution of a Fredholm integral equation. The integral equation is solved for a flat-ended punch and paraboloidal indentations for various values of the nonhomogeneity parameter, and the effects of nonhomogeneity in elastic behaviour on stresses have been shown graphically. The results of the associated homogeneous case are readily available from the results of the present study.

The large-amplitude oscillations and buckling of an anisotropic cylindrical shell subjected to the initial inplane biaxial normal stresses have been analysed. The concept of anisotropy used by Lekhnitsky has been introduced into the field equations for cylindrical shells of isotropic material deduced by Donnell. The method of Galerkin and the method of successive approximation have been used to obtain the desired approximate solution. The expression for the critical loads for the buckling of anisotropic cylindrical shells has been obtained during intermediate stages of analysis. Some relevant frequency response graphs of the obtained solution are also presented. The minimum critical loads for various classes of anisotropy have also been given at the end of the discussion, to exhibit the effects of large deflections and imperfections on elastic buckling.

The movement of the interface between two immiscible fluids flowing through a porous medium is discussed. It is assumed that one of the fluids, which is a liquid, is much more viscous than the other. The problem is transformed by replacing the pressure with an integral of pressure with respect to time. Singularities of pressure and the transformed variable are seen to be related.

Some two-dimensional problems may be solved by comparing the singularities of certain analytic functions, one of which is derived from the new variable. The implications of the approach of a singularity to the moving boundary are examined.

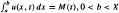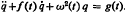An exact invariant is found for the one-dimensional oscillator with equation of motion . The method used is that of linear canonical transformations with time-dependent coeffcients. This is a new approach to the problem and has the advantage of simplicity. When f(t) and g(t) are zero, the invariant is related to the well-known Lewis invariant. The significance of extension to higher dimension of these results is indicated, in particular for the existence of non-invariance dynamical symmetry groups.

In this paper we establish the existence of solutions of a more general class of stochastic integral equation of Volterra type. The main tools used here are the measure of noncompactness and the fixed point theorem of Darbo. The results generalize the results of Tsokos and Padgett [9] and Szynal and Wedrychowicz [7]. An application to a stochastic model arising in chemotherapy is discussed.

We consider some general switching inequalities of Brenner and Alzer. It is shown that Brenner's Theorem B below does not hold in general without further conditions. A simple proof is given of Alzer's Corollary D.