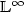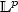Refine search
Actions for selected content:
6997 results in Mathematical modeling and methods
RELIABILITY ANALYSIS OF A SIMPLE REPAIRABLE SYSTEM
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 52 / Issue 2 / October 2010
- Published online by Cambridge University Press:
- 05 September 2011, pp. 203-217
-
- Article
-
- You have access
- Export citation
Homogenization of quasilinear optimal control problemsinvolving a thick multilevel junction of type 3 : 2 : 1∗
-
- Journal:
- ESAIM: Control, Optimisation and Calculus of Variations / Volume 18 / Issue 2 / April 2012
- Published online by Cambridge University Press:
- 26 August 2011, pp. 583-610
- Print publication:
- April 2012
-
- Article
- Export citation
Cell centered Galerkin methods for diffusive problems
-
- Journal:
- ESAIM: Mathematical Modelling and Numerical Analysis / Volume 46 / Issue 1 / January 2012
- Published online by Cambridge University Press:
- 24 August 2011, pp. 111-144
- Print publication:
- January 2012
-
- Article
- Export citation
SURFACE TEMPERATURE RECONSTRUCTION BASED ON THE THERMOCAPILLARY EFFECT
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 52 / Issue 2 / October 2010
- Published online by Cambridge University Press:
- 19 August 2011, pp. 146-159
-
- Article
-
- You have access
- Export citation
A Hölder infinity Laplacian
-
- Journal:
- ESAIM: Control, Optimisation and Calculus of Variations / Volume 18 / Issue 3 / July 2012
- Published online by Cambridge University Press:
- 17 August 2011, pp. 799-835
- Print publication:
- July 2012
-
- Article
- Export citation
Linearization techniques for $\mathbb{L}^{\infty}$
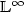 See PDF-control problemsand dynamic programming principles in classical and $\mathbb{L}^{\infty}$
See PDF-control problemsand dynamic programming principles in classical and $\mathbb{L}^{\infty}$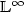 See PDF-control problems
See PDF-control problems
-
- Journal:
- ESAIM: Control, Optimisation and Calculus of Variations / Volume 18 / Issue 3 / July 2012
- Published online by Cambridge University Press:
- 17 August 2011, pp. 836-855
- Print publication:
- July 2012
-
- Article
- Export citation
BOUNDS FOR HARDY DIFFERENCES
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 52 / Issue 2 / October 2010
- Published online by Cambridge University Press:
- 08 August 2011, pp. 218-224
-
- Article
-
- You have access
- Export citation

Noise-Induced Phenomena in the Environmental Sciences
-
- Published online:
- 05 August 2011
- Print publication:
- 20 June 2011
STABILITY ANALYSIS OF A LOTKA–VOLTERRA TYPE PREDATOR–PREY SYSTEM INVOLVING ALLEE EFFECTS
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 52 / Issue 2 / October 2010
- Published online by Cambridge University Press:
- 03 August 2011, pp. 139-145
-
- Article
-
- You have access
- Export citation
CONTACT PROBLEMS FOR NONLINEARLY ELASTIC MATERIALS: WEAK SOLVABILITY INVOLVING DUAL LAGRANGE MULTIPLIERS
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 52 / Issue 2 / October 2010
- Published online by Cambridge University Press:
- 03 August 2011, pp. 160-178
-
- Article
-
- You have access
- Export citation
On the stability of Bravais lattices and their Cauchy–Born approximations*
-
- Journal:
- ESAIM: Mathematical Modelling and Numerical Analysis / Volume 46 / Issue 1 / January 2012
- Published online by Cambridge University Press:
- 26 July 2011, pp. 81-110
- Print publication:
- January 2012
-
- Article
- Export citation
Sufficient optimality conditions and semi-smooth newton methodsfor optimal control of stationary variational inequalities
-
- Journal:
- ESAIM: Control, Optimisation and Calculus of Variations / Volume 18 / Issue 2 / April 2012
- Published online by Cambridge University Press:
- 22 July 2011, pp. 520-547
- Print publication:
- April 2012
-
- Article
- Export citation
A general perturbation formula for electromagnetic fields in presence of low volume scatterers
-
- Journal:
- ESAIM: Mathematical Modelling and Numerical Analysis / Volume 45 / Issue 6 / November 2011
- Published online by Cambridge University Press:
- 22 July 2011, pp. 1193-1218
- Print publication:
- November 2011
-
- Article
- Export citation
Numerical approximation of effective coefficientsin stochastic homogenization of discrete elliptic equations
-
- Journal:
- ESAIM: Mathematical Modelling and Numerical Analysis / Volume 46 / Issue 1 / January 2012
- Published online by Cambridge University Press:
- 22 July 2011, pp. 1-38
- Print publication:
- January 2012
-
- Article
- Export citation
A numerical minimization scheme for the complexHelmholtz equation
-
- Journal:
- ESAIM: Mathematical Modelling and Numerical Analysis / Volume 46 / Issue 1 / January 2012
- Published online by Cambridge University Press:
- 22 July 2011, pp. 39-57
- Print publication:
- January 2012
-
- Article
- Export citation
Rayleigh principle for linear Hamiltonian systems withoutcontrollability∗
-
- Journal:
- ESAIM: Control, Optimisation and Calculus of Variations / Volume 18 / Issue 2 / April 2012
- Published online by Cambridge University Press:
- 22 July 2011, pp. 501-519
- Print publication:
- April 2012
-
- Article
- Export citation
Exponential convergence for a convexifyingequation
-
- Journal:
- ESAIM: Control, Optimisation and Calculus of Variations / Volume 18 / Issue 3 / July 2012
- Published online by Cambridge University Press:
- 22 July 2011, pp. 611-620
- Print publication:
- July 2012
-
- Article
- Export citation
First variation of the generalcurvature-dependent surface energy
-
- Journal:
- ESAIM: Mathematical Modelling and Numerical Analysis / Volume 46 / Issue 1 / January 2012
- Published online by Cambridge University Press:
- 22 July 2011, pp. 59-79
- Print publication:
- January 2012
-
- Article
- Export citation
REGULARITY OF SOLUTIONS TO A TIME-FRACTIONAL DIFFUSION EQUATION
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 52 / Issue 2 / October 2010
- Published online by Cambridge University Press:
- 18 July 2011, pp. 123-138
-
- Article
-
- You have access
- Export citation
Convergence of Cell Based Finite Volume Discretizationsfor Problems of Control in the Conduction Coefficients
-
- Journal:
- ESAIM: Mathematical Modelling and Numerical Analysis / Volume 45 / Issue 6 / November 2011
- Published online by Cambridge University Press:
- 28 June 2011, pp. 1059-1080
- Print publication:
- November 2011
-
- Article
- Export citation