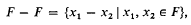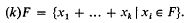Refine listing
Actions for selected content:
152 results in 05Bxx
Transposable and symmetrizable matrices
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 29 / Issue 4 / June 1980
- Published online by Cambridge University Press:
- 09 April 2009, pp. 469-474
- Print publication:
- June 1980
-
- Article
-
- You have access
- Export citation
Bhaskar Rao designs from cyclotomy
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 29 / Issue 4 / June 1980
- Published online by Cambridge University Press:
- 09 April 2009, pp. 425-430
- Print publication:
- June 1980
-
- Article
-
- You have access
- Export citation
Some infinite classes of Hadamard matrices
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 29 / Issue 2 / March 1980
- Published online by Cambridge University Press:
- 09 April 2009, pp. 235-242
- Print publication:
- March 1980
-
- Article
-
- You have access
- Export citation
Balanced binary arrays iii: the hexagonal grid
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics / Volume 28 / Issue 4 / December 1979
- Published online by Cambridge University Press:
- 09 April 2009, pp. 479-498
- Print publication:
- December 1979
-
- Article
-
- You have access
- Export citation
Resolvable (r, λ)-designs and the Fisher inequality
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics / Volume 28 / Issue 4 / December 1979
- Published online by Cambridge University Press:
- 09 April 2009, pp. 471-478
- Print publication:
- December 1979
-
- Article
-
- You have access
- Export citation
On transitive commutative idempotent quasigroups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics / Volume 27 / Issue 4 / June 1979
- Published online by Cambridge University Press:
- 09 April 2009, pp. 411-429
- Print publication:
- June 1979
-
- Article
-
- You have access
- Export citation
A series of BIB designs
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics / Volume 27 / Issue 1 / February 1979
- Published online by Cambridge University Press:
- 09 April 2009, pp. 88-90
- Print publication:
- February 1979
-
- Article
-
- You have access
- Export citation
On the structure and existence of some amicable orthogonal designs
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics / Volume 25 / Issue 1 / February 1978
- Published online by Cambridge University Press:
- 09 April 2009, pp. 118-128
- Print publication:
- February 1978
-
- Article
-
- You have access
- Export citation
Recursive constructions for equidistant permutation arrays
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics / Volume 24 / Issue 2 / September 1977
- Published online by Cambridge University Press:
- 09 April 2009, pp. 216-223
- Print publication:
- September 1977
-
- Article
-
- You have access
- Export citation
Note on difference-covers that are not k-sum-covers
- Part of
-
- Journal:
- Mathematika / Volume 21 / Issue 1 / June 1974
- Published online by Cambridge University Press:
- 26 February 2010, pp. 107-109
- Print publication:
- June 1974
-
- Article
- Export citation
The realization of distances within sets in Euclidean space
- Part of
-
- Journal:
- Mathematika / Volume 19 / Issue 1 / June 1972
- Published online by Cambridge University Press:
- 26 February 2010, pp. 1-24
- Print publication:
- June 1972
-
- Article
- Export citation
Properties of finite character of independence spaces
- Part of
-
- Journal:
- Mathematika / Volume 18 / Issue 2 / December 1971
- Published online by Cambridge University Press:
- 26 February 2010, pp. 201-208
- Print publication:
- December 1971
-
- Article
- Export citation


 ,
,