Refine listing
Actions for selected content:
152 results in 05Bxx
A new proof of the Doyen-Wilson theorem
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 47 / Issue 1 / August 1989
- Published online by Cambridge University Press:
- 09 April 2009, pp. 32-42
- Print publication:
- August 1989
-
- Article
-
- You have access
- Export citation
An infinite class of Hadamard matrices
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 46 / Issue 3 / June 1989
- Published online by Cambridge University Press:
- 09 April 2009, pp. 384-394
- Print publication:
- June 1989
-
- Article
-
- You have access
- Export citation
Some new series of Hadamard matrices
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 46 / Issue 3 / June 1989
- Published online by Cambridge University Press:
- 09 April 2009, pp. 371-383
- Print publication:
- June 1989
-
- Article
-
- You have access
- Export citation
A note on group divisible designs with mutually orthogonal resolutions
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 44 / Issue 3 / June 1988
- Published online by Cambridge University Press:
- 09 April 2009, pp. 397-401
- Print publication:
- June 1988
-
- Article
-
- You have access
- Export citation
The existence of a class of Kirkman squares of index 2
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 44 / Issue 1 / February 1988
- Published online by Cambridge University Press:
- 09 April 2009, pp. 33-41
- Print publication:
- February 1988
-
- Article
-
- You have access
- Export citation
Recursive constructions and some properties of twofold designs with block size four
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 44 / Issue 1 / February 1988
- Published online by Cambridge University Press:
- 09 April 2009, pp. 64-70
- Print publication:
- February 1988
-
- Article
-
- You have access
- Export citation
The Hadamard conjecture and integer lattices
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 43 / Issue 2 / October 1987
- Published online by Cambridge University Press:
- 09 April 2009, pp. 257-267
- Print publication:
- October 1987
-
- Article
-
- You have access
- Export citation
Sequential binary arrays and circulant matrices
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 42 / Issue 3 / June 1987
- Published online by Cambridge University Press:
- 09 April 2009, pp. 330-348
- Print publication:
- June 1987
-
- Article
-
- You have access
- Export citation
Incomplete self-orthogonal latin squares
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 42 / Issue 3 / June 1987
- Published online by Cambridge University Press:
- 09 April 2009, pp. 365-384
- Print publication:
- June 1987
-
- Article
-
- You have access
- Export citation
Exact coverings of triples with specified longest block length
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 42 / Issue 3 / June 1987
- Published online by Cambridge University Press:
- 09 April 2009, pp. 409-420
- Print publication:
- June 1987
-
- Article
-
- You have access
- Export citation
Construction methods for Bhaskar Rao and related designs
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 42 / Issue 1 / February 1987
- Published online by Cambridge University Press:
- 09 April 2009, pp. 5-30
- Print publication:
- February 1987
-
- Article
-
- You have access
- Export citation
Triple systems with a fixed number of repeated triples
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 41 / Issue 2 / October 1986
- Published online by Cambridge University Press:
- 09 April 2009, pp. 180-187
- Print publication:
- October 1986
-
- Article
-
- You have access
- Export citation
A few more balanced Room squares
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 39 / Issue 3 / December 1985
- Published online by Cambridge University Press:
- 09 April 2009, pp. 344-352
- Print publication:
- December 1985
-
- Article
-
- You have access
- Export citation
Indecomposable 1-factorizations of the complete multigraph
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 39 / Issue 3 / December 1985
- Published online by Cambridge University Press:
- 09 April 2009, pp. 334-343
- Print publication:
- December 1985
-
- Article
-
- You have access
- Export citation
Reducible 2 – (11, 5, 4) and 3 – (12, 6, 4) designs
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 39 / Issue 2 / October 1985
- Published online by Cambridge University Press:
- 09 April 2009, pp. 194-215
- Print publication:
- October 1985
-
- Article
-
- You have access
- Export citation
The projective geometry arising from a hollow module
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 37 / Issue 3 / December 1984
- Published online by Cambridge University Press:
- 09 April 2009, pp. 351-357
- Print publication:
- December 1984
-
- Article
-
- You have access
- Export citation
Families of sets on a finite set
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 37 / Issue 3 / December 1984
- Published online by Cambridge University Press:
- 09 April 2009, pp. 405-412
- Print publication:
- December 1984
-
- Article
-
- You have access
- Export citation
Six pairwise orthogonal latin squares of order 69
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 37 / Issue 1 / August 1984
- Published online by Cambridge University Press:
- 09 April 2009, pp. 1-3
- Print publication:
- August 1984
-
- Article
-
- You have access
- Export citation
Pair-packings and projective planes
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 37 / Issue 1 / August 1984
- Published online by Cambridge University Press:
- 09 April 2009, pp. 27-38
- Print publication:
- August 1984
-
- Article
-
- You have access
- Export citation
Room n-cubes of lowe order
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 36 / Issue 2 / April 1984
- Published online by Cambridge University Press:
- 09 April 2009, pp. 237-252
- Print publication:
- April 1984
-
- Article
-
- You have access
- Export citation
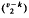 when
when 