In the full rectangular version of Gilbert's planar tessellation (see Gilbert (1967), Mackisack and Miles (1996), and Burridge et al. (2013)), lines extend either horizontally (with east- and west-growing rays) or vertically (north- and south-growing rays) from seed points which form a stationary Poisson point process, each ray stopping when it meets another ray that has blocked its path. In the half-Gilbert rectangular version, east- and south-growing rays, whilst having the potential to block each other, do not interact with west and north rays, and vice versa. East- and south-growing rays have a reciprocality of blocking, as do west and north. In this paper we significantly expand and simplify the half-Gilbert analytic results that we gave in Burridge et al. (2013). We also show how the idea of reciprocality of blocking between rays can be used in a much wider context, with rays not necessarily orthogonal and with seeds that produce more than two rays.

In this paper, we consider the so-called “Furstenberg set problem” in high dimensions. First, following Wolff’s work on the two-dimensional real case, we provide “reasonable” upper bounds for the problem for $\mathbb{R}$ or $\mathbb{F}_{p}$. Next we study the “critical” case and improve the “trivial” exponent by ${\rm\Omega}(1/n^{2})$ for $\mathbb{F}_{p}^{n}$. Our key tool in obtaining this lower bound is a theorem about how things behave when the Loomis–Whitney inequality is nearly sharp, as it helps us to reduce the problem to dimension two.

We show that if a Barker sequence of length $n>13$ exists, then either n $=$ 3 979 201 339 721749 133 016 171 583 224 100, or $n > 4\cdot 10^{33}$ . This improves the lower bound on the length of a long Barker sequence by a factor of nearly $2000$ . We also obtain eighteen additional integers $n<10^{50}$ that cannot be ruled out as the length of a Barker sequence, and find more than 237 000 additional candidates $n<10^{100}$ . These results are obtained by completing extensive searches for Wieferich prime pairs and using them, together with a number of arithmetic restrictions on $n$ , to construct qualifying integers below a given bound. We also report on some updated computations regarding open cases of the circulant Hadamard matrix problem.

While the intersection of the Grassmannian Bruhat decompositions for all coordinate flags is an intractable mess, it turns out that the intersection of only the cyclic shifts of one Bruhat decomposition has many of the good properties of the Bruhat and Richardson decompositions. This decomposition coincides with the projection of the Richardson stratification of the flag manifold, studied by Lusztig, Rietsch, Brown–Goodearl–Yakimov and the present authors. However, its cyclic-invariance is hidden in this description. Postnikov gave many cyclic-invariant ways to index the strata, and we give a new one, by a subset of the affine Weyl group we call bounded juggling patterns. We call the strata positroid varieties. Applying results from [A. Knutson, T. Lam and D. Speyer, Projections of Richardson varieties, J. Reine Angew. Math., to appear, arXiv:1008.3939 [math.AG]], we show that positroid varieties are normal, Cohen–Macaulay, have rational singularities, and are defined as schemes by the vanishing of Plücker coordinates. We prove that their associated cohomology classes are represented by affine Stanley functions. This latter fact lets us connect Postnikov’s and Buch–Kresch–Tamvakis’ approaches to quantum Schubert calculus.

In a recent paper of Ellenberg, Oberlin, and Tao [The Kakeya set and maximal conjectures for algebraic varieties over finite fields. Mathematika 56 (2010), 1–25], the authors asked whether there are Besicovitch phenomena in ${ \mathbb{F} }_{q} \mathop{[[t] ] }\nolimits ^{n} $. In this paper, we answer their question in the affirmative by explicitly constructing a Kakeya set of measure zero in ${ \mathbb{F} }_{q} \mathop{[[t] ] }\nolimits ^{n} $. Furthermore, we prove that any Kakeya set in ${ \mathbb{F} }_{q} \mathop{[[t] ] }\nolimits ^{2} $ or ${ \mathbb{Z} }_{p}^{2} $ is of Minkowski dimension 2.

We investigate the ray-length distributions for two different rectangular versions of Gilbert's tessellation (see Gilbert (1967)). In the full rectangular version, lines extend either horizontally (east- and west-growing rays) or vertically (north- and south-growing rays) from seed points which form a Poisson point process, each ray stopping when another ray is met. In the half rectangular version, east- and south-growing rays do not interact with west and north rays. For the half rectangular tessellation, we compute analytically, via recursion, a series expansion for the ray-length distribution, whilst, for the full rectangular version, we develop an accurate simulation technique, based in part on the stopping-set theory for Poisson processes (see Zuyev (1999)), to accomplish the same. We demonstrate the remarkable fact that plots of the two distributions appear to be identical when the intensity of seeds in the half model is twice that in the full model. In this paper we explore this coincidence, mindful of the fact that, for one model, our results are from a simulation (with inherent sampling error). We go on to develop further analytic theory for the half-Gilbert model using stopping-set ideas once again, with some novel features. Using our theory, we obtain exact expressions for the first and second moments of the ray length in the half-Gilbert model. For all practical purposes, these results can be applied to the full-Gilbert model—as much better approximations than those provided by Mackisack and Miles (1996).

We prove an upper bound on sums of squares of minors of $\{+1, -1\}$-matrices. The bound is sharp for Hadamard matrices, a result due to de Launey and Levin [‘$(1,-1)$-matrices with near-extremal properties’, SIAM J. Discrete Math.23(2009), 1422–1440], but our proof is simpler. We give several corollaries relevant to minors of Hadamard matrices.

We raise and investigate the following problem which one can regard as a very close relative of the densest sphere packing problem. If the Euclidean 3-space is partitioned into convex cells each containing a unit ball, how should the shapes of the cells be designed to minimize the average surface area of the cells? In particular, we prove that the average surface area in question is always at least

Tessellations of R 3 that use convex polyhedral cells to fill the space can be extremely complicated. This is especially so for tessellations which are not ‘facet-to-facet’, that is, for those where the facets of a cell do not necessarily coincide with the facets of that cell's neighbours. Adjacency concepts between neighbouring cells (or between neighbouring cell elements) are not easily formulated when facets do not coincide. In this paper we make the first systematic study of these topological relationships when a tessellation of R 3 is not facet-to-facet. The results derived can also be applied to the simpler facet-to-facet case. Our study deals with both random tessellations and deterministic ‘tilings’. Some new theory for planar tessellations is also given.

Mixed-level orthogonal arrays are basic structures in experimental design. We develop three algorithms that compute Rao- and Gilbert-Varshamov-type bounds for mixed-level orthogonal arrays. The computational complexity of the terms involved in the original combinatorial representations of these bounds can grow fast as the parameters of the arrays increase and this justifies the construction of these algorithms. The first is a recursive algorithm that computes the bounds exactly, the second is based on an asymptotic analysis, and the third is a simulation algorithm. They are all based on the representation of the combinatorial expressions that appear in the bounds as expectations involving a symmetric random walk. The Markov property of the underlying random walk gives the recursive formula to compute the expectations. A large deviation (LD) analysis of the expectations provides the asymptotic algorithm. The asymptotically optimal importance sampling (IS) of the same expectation provides the simulation algorithm. Both the LD analysis and the construction of the IS algorithm use a representation of these problems as a sequence of stochastic optimal control problems converging to a limit calculus of a variations problem. The construction of the IS algorithm uses a recently discovered method of using subsolutions to the Hamilton-Jacobi-Bellman equations associated with the limit problem.

The so-called STIT tessellations form a class of homogeneous (spatially stationary) tessellations in R d which are stable under the nesting/iteration operation. In this paper we establish the mixing property for these tessellations and give the decay rate of P(A ∩ M = ∅, T h B ∩ M = ∅) / P(A ∩ Y = ∅)P(B ∩ Y = ∅) − 1, where A and B are both compact connected sets, h is a vector of R d , T h is the corresponding translation operator, and M is a STIT tessellation.

We present new ideas about the type of random tessellation which evolves through successive division of its cells. These ideas are developed in an intuitive way, with many pictures and only a modicum of mathematical formalism–so that the wide application of the ideas is clearly apparent to all readers. A vast number of new tessellation models, with known probability distribution for the volume of the typical cell, follow from the concepts in this paper. There are other interesting models for which results are not presented (or presented only through simulation methods), but these models have illustrative value. A large agenda of further research is opened up by the ideas in this paper.

We discuss n4 configurations of n points and n planes in three-dimensional projective space. These have four points on each plane, and four planes through each point. When the last of the 4n incidences between points and planes happens as a consequence of the preceding 4n−1 the configuration is called a ‘theorem’. Using a graph-theoretic search algorithm we find that there are two 84 and one 94 ‘theorems’. One of these 84 ‘theorems’ was already found by Möbius in 1828, while the 94 ‘theorem’ is related to Desargues’ ten-point configuration. We prove these ‘theorems’ by various methods, and connect them with other questions, such as forbidden minors in graph theory, and sets of electrons that are energy minimal.

For a class of ‘linear’ sudoku solutions, we construct mutually orthogonal families of maximal size for all square orders, and we show that all such solutions must lie in the same orbit of a symmetry group preserving sudoku solutions.

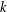
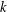
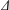
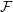
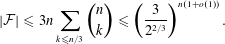
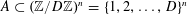
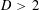
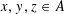
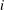
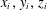
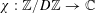
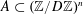
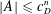
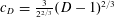
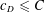
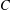
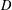
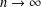
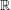
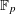
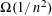
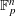
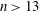
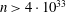
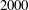
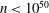
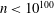
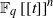
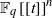
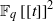
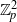
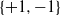
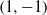
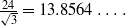
For three points , and 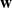in the 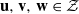n-dimensional space 𝔽nq over the finite field 𝔽q of q elements we give a natural interpretation of an acute angle triangle defined by these points. We obtain an upper bound on the size of a set 𝒵 such that all triples of distinct points define acute angle triangles. A similar question in the real space ℛn dates back to P. Erdős and has been studied by several authors.

A one-dimensional tiling is a bi-infinite string on a finite alphabet, and its tiling semigroup is an inverse semigroup whose elements are marked finite substrings of the tiling. We characterize the structure of these semigroups in the periodic case, in which the tiling is obtained by repetition of a fixed primitive word.

Qualified difference sets (QDS) composed of unions of cyclotomic classes are discussed. An exhaustive computer search for such QDS and modified QDS that also possess the zero residue has been conducted for all powers n=4,6,8 and 10. Two new families were discovered in the case n=8 and some new isolated systems were discovered for n=6 and n=10.