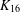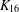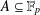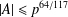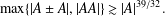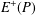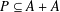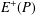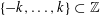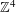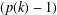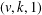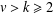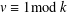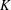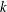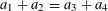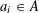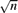Refine listing
Actions for selected content:
152 results in 05Bxx
PERFECT 1-FACTORISATIONS OF
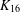 $K_{16}$
$K_{16}$
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 101 / Issue 2 / April 2020
- Published online by Cambridge University Press:
- 07 August 2019, pp. 177-185
- Print publication:
- April 2020
-
- Article
-
- You have access
- Export citation
A NEW SUM–PRODUCT ESTIMATE IN PRIME FIELDS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 100 / Issue 2 / October 2019
- Published online by Cambridge University Press:
- 24 May 2019, pp. 268-280
- Print publication:
- October 2019
-
- Article
-
- You have access
- Export citation
Topological Properties of a Class of Higher-dimensional Self-affine Tiles
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 62 / Issue 4 / December 2019
- Published online by Cambridge University Press:
- 03 May 2019, pp. 727-740
- Print publication:
- December 2019
-
- Article
-
- You have access
- Export citation
Restricted completion of sparse partial Latin squares
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 28 / Issue 5 / September 2019
- Published online by Cambridge University Press:
- 20 February 2019, pp. 675-695
-
- Article
- Export citation
AN ALGORITHM TO CONSTRUCT THE LE DIAGRAM ASSOCIATED TO A GRASSMANN NECKLACE
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 62 / Issue 1 / January 2020
- Published online by Cambridge University Press:
- 18 January 2019, pp. 85-91
-
- Article
-
- You have access
- Export citation
HADAMARD MATRICES AND 1-FACTORIZATIONS OF COMPLETE GRAPHS
- Part of
-
- Journal:
- Mathematika / Volume 65 / Issue 3 / 2019
- Published online by Cambridge University Press:
- 11 February 2019, pp. 488-499
- Print publication:
- 2019
-
- Article
- Export citation
LONELY RUNNERS IN FUNCTION FIELDS
- Part of
-
- Journal:
- Mathematika / Volume 65 / Issue 3 / 2019
- Published online by Cambridge University Press:
- 12 April 2019, pp. 677-701
- Print publication:
- 2019
-
- Article
- Export citation
Multiple Lattice Tilings in Euclidean Spaces
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 62 / Issue 4 / December 2019
- Published online by Cambridge University Press:
- 16 November 2018, pp. 923-929
- Print publication:
- December 2019
-
- Article
-
- You have access
- Export citation
Polynomial Mixing of the Edge-Flip Markov Chain for Unbiased Dyadic Tilings
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 28 / Issue 3 / May 2019
- Published online by Cambridge University Press:
- 31 October 2018, pp. 365-387
-
- Article
- Export citation
TILING WITH PUNCTURED INTERVALS
- Part of
-
- Journal:
- Mathematika / Volume 65 / Issue 2 / 2019
- Published online by Cambridge University Press:
- 29 October 2018, pp. 181-189
- Print publication:
- 2019
-
- Article
- Export citation
CHARACTERIZING HERMITIAN VARIETIES IN THREE- AND FOUR-DIMENSIONAL PROJECTIVE SPACES
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 107 / Issue 1 / August 2019
- Published online by Cambridge University Press:
- 29 October 2018, pp. 1-8
-
- Article
-
- You have access
- Export citation
COORDINATISING PLANES OF PRIME POWER ORDER USING FINITE FIELDS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 106 / Issue 2 / April 2019
- Published online by Cambridge University Press:
- 22 August 2018, pp. 184-199
-
- Article
-
- You have access
- Export citation
RESOLVABLE MENDELSOHN DESIGNS AND FINITE FROBENIUS GROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 98 / Issue 1 / August 2018
- Published online by Cambridge University Press:
- 30 May 2018, pp. 1-13
- Print publication:
- August 2018
-
- Article
-
- You have access
- Export citation
POTENTIALS OF A FROBENIUS-LIKE STRUCTURE
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 60 / Issue 3 / September 2018
- Published online by Cambridge University Press:
- 28 January 2018, pp. 681-693
-
- Article
-
- You have access
- Export citation
COVERS OF GENERALIZED QUADRANGLES
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 60 / Issue 3 / September 2018
- Published online by Cambridge University Press:
- 25 January 2018, pp. 585-601
-
- Article
-
- You have access
- Export citation
ADDITIVE ENERGY AND THE METRIC POISSONIAN PROPERTY
- Part of
-
- Journal:
- Mathematika / Volume 64 / Issue 3 / 2018
- Published online by Cambridge University Press:
- 19 June 2018, pp. 679-700
- Print publication:
- 2018
-
- Article
- Export citation
GENERALISATIONS OF THE DOYEN–WILSON THEOREM
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 97 / Issue 1 / February 2018
- Published online by Cambridge University Press:
- 04 December 2017, pp. 166-167
- Print publication:
- February 2018
-
- Article
-
- You have access
- Export citation
MAXIMUM GENUS EMBEDDINGS OF LATIN SQUARES
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 60 / Issue 2 / May 2018
- Published online by Cambridge University Press:
- 30 October 2017, pp. 495-504
-
- Article
-
- You have access
- Export citation
Monotone Subsequences in High-Dimensional Permutations
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 27 / Issue 1 / January 2018
- Published online by Cambridge University Press:
- 16 October 2017, pp. 69-83
-
- Article
- Export citation
SIMPLE GROUPS, PRODUCT ACTIONS, AND GENERALIZED QUADRANGLES
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 234 / June 2019
- Published online by Cambridge University Press:
- 14 September 2017, pp. 87-126
-
- Article
-
- You have access
- HTML
- Export citation