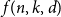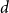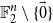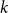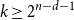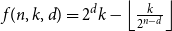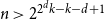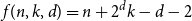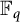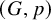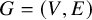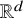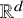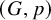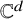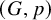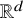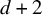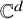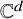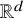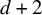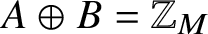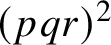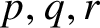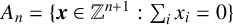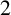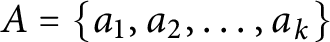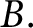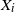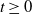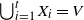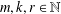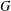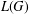Refine listing
Actions for selected content:
152 results in 05Bxx
Subspace coverings with multiplicities
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 32 / Issue 5 / September 2023
- Published online by Cambridge University Press:
- 18 May 2023, pp. 782-795
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A generalization of Kruskal’s theorem on tensor decomposition
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 05 April 2023, e27
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Nearly sharp Lang–Weil bounds for a hypersurface
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 2 / June 2023
- Published online by Cambridge University Press:
- 18 October 2022, pp. 654-664
- Print publication:
- June 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Globally rigid graphs are fully reconstructible
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 10 / 2022
- Published online by Cambridge University Press:
- 07 July 2022, e51
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Undecidability of the Spectral Gap
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 10 / 2022
- Published online by Cambridge University Press:
- 10 June 2022, e14
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Combinatorial and harmonic-analytic methods for integer tilings
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 10 / 2022
- Published online by Cambridge University Press:
- 09 March 2022, e8
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Packable hyperbolic surfaces with symmetries
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 1 / March 2023
- Published online by Cambridge University Press:
- 11 February 2022, pp. 103-113
- Print publication:
- March 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ABELIAN DIFFERENCE SETS AS LATTICE COVERINGS AND LATTICE TILINGS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 106 / Issue 2 / October 2022
- Published online by Cambridge University Press:
- 24 January 2022, pp. 177-184
- Print publication:
- October 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On multiplicative energy of subsets of varieties
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 75 / Issue 1 / February 2023
- Published online by Cambridge University Press:
- 13 January 2022, pp. 322-340
- Print publication:
- February 2023
-
- Article
- Export citation
Asymptotics for the number of standard tableaux of skew shape and for weighted lozenge tilings
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 31 / Issue 4 / July 2022
- Published online by Cambridge University Press:
- 18 October 2021, pp. 550-573
-
- Article
- Export citation
AN APERIODIC TILE WITH EDGE-TO-EDGE ORIENTATIONAL MATCHING RULES
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 22 / Issue 4 / July 2023
- Published online by Cambridge University Press:
- 18 October 2021, pp. 1727-1755
- Print publication:
- July 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On the number of Hadamard matrices via anti-concentration
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 31 / Issue 3 / May 2022
- Published online by Cambridge University Press:
- 10 September 2021, pp. 455-477
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Strongly aperiodic subshifts of finite type on hyperbolic groups
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 42 / Issue 9 / September 2022
- Published online by Cambridge University Press:
- 09 September 2021, pp. 2740-2783
- Print publication:
- September 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Sumsets of semiconvex sets
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 65 / Issue 1 / March 2022
- Published online by Cambridge University Press:
- 26 February 2021, pp. 84-94
- Print publication:
- March 2022
-
- Article
- Export citation
A rainbow blow-up lemma for almost optimally bounded edge-colourings
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 8 / 2020
- Published online by Cambridge University Press:
- 30 October 2020, e37
-
- Article
-
- You have access
- Open access
- Export citation
Beyond Beatty sequences: Complementary lattices
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 64 / Issue 3 / September 2021
- Published online by Cambridge University Press:
- 06 August 2020, pp. 499-511
- Print publication:
- September 2021
-
- Article
- Export citation
Large triangle packings and Tuza’s conjecture in sparse random graphs
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 29 / Issue 5 / September 2020
- Published online by Cambridge University Press:
- 22 July 2020, pp. 757-779
-
- Article
- Export citation
Speed and concentration of the covering time for structured coupon collectors
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 52 / Issue 2 / June 2020
- Published online by Cambridge University Press:
- 15 July 2020, pp. 433-462
- Print publication:
- June 2020
-
- Article
- Export citation
A RAMSEY TYPE RESULT FOR LATIN SQUARES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 101 / Issue 3 / June 2020
- Published online by Cambridge University Press:
- 22 November 2019, pp. 362-366
- Print publication:
- June 2020
-
- Article
-
- You have access
- Export citation
On the number of symbols that forces a transversal
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 29 / Issue 2 / March 2020
- Published online by Cambridge University Press:
- 21 October 2019, pp. 234-240
-
- Article
- Export citation