Refine listing
Actions for selected content:
138 results in 68Mxx
A brokered market with heterogeneous suppliers and consumers
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 36 / Issue 2 / June 1999
- Published online by Cambridge University Press:
- 14 July 2016, pp. 512-522
- Print publication:
- June 1999
-
- Article
- Export citation
Loss networks and Markov random fields
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 36 / Issue 2 / June 1999
- Published online by Cambridge University Press:
- 14 July 2016, pp. 403-414
- Print publication:
- June 1999
-
- Article
- Export citation
Asymptotics of palm-stationary buffer content distributions in fluid flow queues
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 31 / Issue 1 / March 1999
- Published online by Cambridge University Press:
- 01 July 2016, pp. 235-253
- Print publication:
- March 1999
-
- Article
- Export citation
Optimal dynamic scheduling of a general class of parallel-processing queueing systems
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 30 / Issue 4 / December 1998
- Published online by Cambridge University Press:
- 01 July 2016, pp. 1130-1156
- Print publication:
- December 1998
-
- Article
- Export citation
Concavity of queueing systems with NBU service times
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 30 / Issue 2 / June 1998
- Published online by Cambridge University Press:
- 01 July 2016, pp. 551-567
- Print publication:
- June 1998
-
- Article
- Export citation
Asymptotically achievable performance in ATM networks
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 30 / Issue 2 / June 1998
- Published online by Cambridge University Press:
- 01 July 2016, pp. 568-585
- Print publication:
- June 1998
-
- Article
- Export citation
On the Inverse of Erlang's Function
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 35 / Issue 1 / March 1998
- Published online by Cambridge University Press:
- 14 July 2016, pp. 246-252
- Print publication:
- March 1998
-
- Article
- Export citation
A product-form ‘loss network' with a form of queueing
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 34 / Issue 4 / December 1997
- Published online by Cambridge University Press:
- 14 July 2016, pp. 1075-1078
- Print publication:
- December 1997
-
- Article
- Export citation
Non-Skip-Free M/G/1 and G/M/1 Type Markov Chains
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 29 / Issue 3 / September 1997
- Published online by Cambridge University Press:
- 01 July 2016, pp. 733-758
- Print publication:
- September 1997
-
- Article
- Export citation
Stochastic scheduling for a two-machine open shop
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 34 / Issue 3 / September 1997
- Published online by Cambridge University Press:
- 14 July 2016, pp. 733-744
- Print publication:
- September 1997
-
- Article
- Export citation
Unification of Software Reliability Models by Self-Exciting Point Processes
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 29 / Issue 2 / June 1997
- Published online by Cambridge University Press:
- 01 July 2016, pp. 337-352
- Print publication:
- June 1997
-
- Article
- Export citation
A correspondence between product-form batch-movement queueing networks and single-movement networks
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 34 / Issue 1 / March 1997
- Published online by Cambridge University Press:
- 14 July 2016, pp. 160-175
- Print publication:
- March 1997
-
- Article
- Export citation
Braess's paradox in a loss network
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 34 / Issue 1 / March 1997
- Published online by Cambridge University Press:
- 14 July 2016, pp. 155-159
- Print publication:
- March 1997
-
- Article
- Export citation
Solution of finite QBD processes
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 33 / Issue 4 / December 1996
- Published online by Cambridge University Press:
- 14 July 2016, pp. 1003-1010
- Print publication:
- December 1996
-
- Article
- Export citation
Dynamic routing and jockeying controls in a two-station queueing system
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 28 / Issue 4 / December 1996
- Published online by Cambridge University Press:
- 01 July 2016, pp. 1201-1226
- Print publication:
- December 1996
-
- Article
- Export citation
Optimal policies for scheduling repairs and allocating heterogeneous servers
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 33 / Issue 2 / September 1996
- Published online by Cambridge University Press:
- 14 July 2016, pp. 536-547
- Print publication:
- September 1996
-
- Article
- Export citation
Rate of convergence of the fluid approximation for generalized Jackson networks
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 33 / Issue 3 / September 1996
- Published online by Cambridge University Press:
- 14 July 2016, pp. 804-814
- Print publication:
- September 1996
-
- Article
- Export citation
Buffer overflow asymptotics for a buffer handling many traffic sources
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 33 / Issue 3 / September 1996
- Published online by Cambridge University Press:
- 14 July 2016, pp. 886-903
- Print publication:
- September 1996
-
- Article
- Export citation
Asymptotic expansions for functionals of dilation of point processes
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 33 / Issue 2 / September 1996
- Published online by Cambridge University Press:
- 14 July 2016, pp. 573-591
- Print publication:
- September 1996
-
- Article
- Export citation
Busy period in GIX/G/∞
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 33 / Issue 3 / September 1996
- Published online by Cambridge University Press:
- 14 July 2016, pp. 815-829
- Print publication:
- September 1996
-
- Article
- Export citation
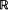 and
and 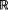
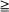 2, under transparent conditions, close to minimal. Formulas for higher-order derivatives allow one to construct asymptotical expansions. The results can be useful in sensitivity analysis, in light traffic theory for queues and for computation by simulation of derivatives at positive intensity, while the computation of the derivatives via statistical estimation of the functional itself and its increments usually gives poor results.
2, under transparent conditions, close to minimal. Formulas for higher-order derivatives allow one to construct asymptotical expansions. The results can be useful in sensitivity analysis, in light traffic theory for queues and for computation by simulation of derivatives at positive intensity, while the computation of the derivatives via statistical estimation of the functional itself and its increments usually gives poor results.