Refine listing
Actions for selected content:
138 results in 68Mxx
Heavy Tails in Queueing Systems: Impact of Parallelism on Tail Performance
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 50 / Issue 1 / March 2013
- Published online by Cambridge University Press:
- 30 January 2018, pp. 127-150
- Print publication:
- March 2013
-
- Article
-
- You have access
- Export citation
Exact-Order Asymptotic Analysis for Closed Queueing Networks
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 49 / Issue 2 / June 2012
- Published online by Cambridge University Press:
- 04 February 2016, pp. 503-520
- Print publication:
- June 2012
-
- Article
-
- You have access
- Export citation
Hurst Index of Functions of Long-Range-Dependent Markov Chains
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 49 / Issue 2 / June 2012
- Published online by Cambridge University Press:
- 04 February 2016, pp. 451-471
- Print publication:
- June 2012
-
- Article
-
- You have access
- Export citation
A Recurrent Solution of PH/M/c/N-Like and PH/M/c-Like Queues
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 49 / Issue 1 / March 2012
- Published online by Cambridge University Press:
- 04 February 2016, pp. 84-99
- Print publication:
- March 2012
-
- Article
-
- You have access
- Export citation
Stationarity and control of a tandem fluid network with fractional Brownian motion input
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 43 / Issue 3 / September 2011
- Published online by Cambridge University Press:
- 01 July 2016, pp. 847-874
- Print publication:
- September 2011
-
- Article
-
- You have access
- Export citation
Duality results for Markov-modulated fluid flow models
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 48 / Issue A / August 2011
- Published online by Cambridge University Press:
- 14 July 2016, pp. 309-318
- Print publication:
- August 2011
-
- Article
-
- You have access
- Export citation
Asymptotic Fluid Optimality and Efficiency of the Tracking Policy for Bandwidth-Sharing Networks
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 48 / Issue 1 / March 2011
- Published online by Cambridge University Press:
- 14 July 2016, pp. 90-113
- Print publication:
- March 2011
-
- Article
-
- You have access
- Export citation
Low degree connectivity of ad-hoc networks via percolation
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 42 / Issue 2 / June 2010
- Published online by Cambridge University Press:
- 01 July 2016, pp. 559-576
- Print publication:
- June 2010
-
- Article
-
- You have access
- Export citation
Insensitive Bounds for the Moments of the Sojourn Times in M/GI Systems Under State-Dependent Processor Sharing
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 42 / Issue 1 / March 2010
- Published online by Cambridge University Press:
- 01 July 2016, pp. 246-267
- Print publication:
- March 2010
-
- Article
-
- You have access
- Export citation
Optimal Control of a Stochastic Processing System Driven by a Fractional Brownian Motion Input
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 42 / Issue 1 / March 2010
- Published online by Cambridge University Press:
- 01 July 2016, pp. 183-209
- Print publication:
- March 2010
-
- Article
-
- You have access
- Export citation
Fcfs infinite bipartite matching of servers and customers
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 41 / Issue 3 / September 2009
- Published online by Cambridge University Press:
- 01 July 2016, pp. 695-730
- Print publication:
- September 2009
-
- Article
-
- You have access
- Export citation
Importance Sampling for Failure Probabilities in Computing and Data Transmission
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 46 / Issue 3 / September 2009
- Published online by Cambridge University Press:
- 14 July 2016, pp. 768-790
- Print publication:
- September 2009
-
- Article
-
- You have access
- Export citation
Job replication on multiserver systems
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 41 / Issue 2 / June 2009
- Published online by Cambridge University Press:
- 01 July 2016, pp. 546-575
- Print publication:
- June 2009
-
- Article
-
- You have access
- Export citation
SCHEDULING A HETEROGENEOUS SET OF TRAINS OVER A SINGLE LINE TRACK USING LAGRANGIAN RELAXATION
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 50 / Issue 2 / October 2008
- Published online by Cambridge University Press:
- 01 October 2008, pp. 266-281
-
- Article
-
- You have access
- Export citation
FROBENIUS CIRCULANT GRAPHS OF VALENCY FOUR
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 85 / Issue 2 / October 2008
- Published online by Cambridge University Press:
- 01 October 2008, pp. 269-282
- Print publication:
- October 2008
-
- Article
-
- You have access
- Export citation
Dynamic Distributed Scheduling in Random Access Networks
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 45 / Issue 2 / June 2008
- Published online by Cambridge University Press:
- 14 July 2016, pp. 297-313
- Print publication:
- June 2008
-
- Article
-
- You have access
- Export citation
Transient Moments of the TCP Window Size Process
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 45 / Issue 1 / March 2008
- Published online by Cambridge University Press:
- 14 July 2016, pp. 163-175
- Print publication:
- March 2008
-
- Article
-
- You have access
- Export citation
A Unifying Conservation Law for Single-Server Queues
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 44 / Issue 4 / December 2007
- Published online by Cambridge University Press:
- 14 July 2016, pp. 1078-1087
- Print publication:
- December 2007
-
- Article
-
- You have access
- Export citation
Zero-automatic queues and product form
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 39 / Issue 2 / June 2007
- Published online by Cambridge University Press:
- 01 July 2016, pp. 429-461
- Print publication:
- June 2007
-
- Article
-
- You have access
- Export citation
Large deviation properties of constant rate data streams sharing a buffer with long-range dependent traffic in critical loading
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 39 / Issue 2 / June 2007
- Published online by Cambridge University Press:
- 01 July 2016, pp. 407-428
- Print publication:
- June 2007
-
- Article
-
- You have access
- Export citation
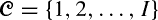 and an infinite sequence of servers of types
and an infinite sequence of servers of types 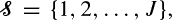 where a server of type
where a server of type 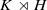 such that
such that 