Refine listing
Actions for selected content:
138 results in 68Mxx
Spectral analysis of M/G/1 and G/M/1 type Markov chains
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 28 / Issue 1 / March 1996
- Published online by Cambridge University Press:
- 01 July 2016, pp. 114-165
- Print publication:
- March 1996
-
- Article
- Export citation
Performance analysis of the discrete-time GI/Geom/1/N queue
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 33 / Issue 1 / March 1996
- Published online by Cambridge University Press:
- 14 July 2016, pp. 239-255
- Print publication:
- March 1996
-
- Article
- Export citation
The performance of the move-to-front scheme under some particular forms of Markov requests
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 32 / Issue 4 / December 1995
- Published online by Cambridge University Press:
- 14 July 2016, pp. 1089-1102
- Print publication:
- December 1995
-
- Article
- Export citation
Transient characteristics of an M/M/∞ system
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 27 / Issue 3 / September 1995
- Published online by Cambridge University Press:
- 01 July 2016, pp. 862-888
- Print publication:
- September 1995
-
- Article
- Export citation
Optimal software release policy based on a two-person game of timing
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 32 / Issue 2 / June 1995
- Published online by Cambridge University Press:
- 14 July 2016, pp. 470-481
- Print publication:
- June 1995
-
- Article
- Export citation
Asymptotic analysis of single resource loss systems in heavy traffic, with applications to integrated networks
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 27 / Issue 1 / March 1995
- Published online by Cambridge University Press:
- 01 July 2016, pp. 273-292
- Print publication:
- March 1995
-
- Article
- Export citation
Exponential upper bounds via martingales for multiplexers with Markovian arrivals
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 31 / Issue 4 / December 1994
- Published online by Cambridge University Press:
- 14 July 2016, pp. 1049-1060
- Print publication:
- December 1994
-
- Article
- Export citation
The optimality of LEPT in parallel machine scheduling
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 31 / Issue 3 / September 1994
- Published online by Cambridge University Press:
- 14 July 2016, pp. 788-796
- Print publication:
- September 1994
-
- Article
- Export citation
Optimality of the round-robin routing policy
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 31 / Issue 2 / June 1994
- Published online by Cambridge University Press:
- 14 July 2016, pp. 466-475
- Print publication:
- June 1994
-
- Article
- Export citation
Exact and ordinary lumpability in finite Markov chains
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 31 / Issue 1 / March 1994
- Published online by Cambridge University Press:
- 14 July 2016, pp. 59-75
- Print publication:
- March 1994
-
- Article
- Export citation
The matrix M/M/∞ system: retrial models and Markov Modulated sources
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 25 / Issue 2 / June 1993
- Published online by Cambridge University Press:
- 01 July 2016, pp. 453-471
- Print publication:
- June 1993
-
- Article
- Export citation
Analysis of an M/G/1/K/N queue
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 30 / Issue 2 / June 1993
- Published online by Cambridge University Press:
- 14 July 2016, pp. 446-454
- Print publication:
- June 1993
-
- Article
- Export citation
Scheduling and stability aspects of a general class of parallel processing systems
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 25 / Issue 1 / March 1993
- Published online by Cambridge University Press:
- 01 July 2016, pp. 176-202
- Print publication:
- March 1993
-
- Article
- Export citation
Virtual customers in sensitivity and light traffic analysis via Campbell's formula for point processes
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 25 / Issue 1 / March 1993
- Published online by Cambridge University Press:
- 01 July 2016, pp. 221-234
- Print publication:
- March 1993
-
- Article
- Export citation
On a job resequencing issue in parallel processor stochastic scheduling
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 24 / Issue 4 / December 1992
- Published online by Cambridge University Press:
- 01 July 2016, pp. 915-933
- Print publication:
- December 1992
-
- Article
- Export citation
On the serial correlation for number in system in the stationary GI/M/1 bulk arrival and GI/Em /1 queues
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 29 / Issue 2 / June 1992
- Published online by Cambridge University Press:
- 14 July 2016, pp. 404-417
- Print publication:
- June 1992
-
- Article
- Export citation
Time-dependent process of M/G/1 vacation models with exhaustive service
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 29 / Issue 2 / June 1992
- Published online by Cambridge University Press:
- 14 July 2016, pp. 418-429
- Print publication:
- June 1992
-
- Article
- Export citation
Stochastic convexity of sums of i.i.d. non-negative random variables with applications
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 29 / Issue 1 / March 1992
- Published online by Cambridge University Press:
- 14 July 2016, pp. 156-167
- Print publication:
- March 1992
-
- Article
- Export citation
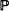 [queue length
[queue length 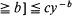 for any
for any 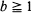 where
where 