Refine listing
Actions for selected content:
29 results in 46Mxx
Higher Dimensional Cohomology of Weighted Sequence Algebras
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 75 / Issue 1 / August 2003
- Published online by Cambridge University Press:
- 09 April 2009, pp. 57-68
- Print publication:
- August 2003
-
- Article
-
- You have access
- Export citation
Categorical constructions in C*-algebra theory
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 73 / Issue 1 / August 2002
- Published online by Cambridge University Press:
- 09 April 2009, pp. 97-114
- Print publication:
- August 2002
-
- Article
-
- You have access
- Export citation
Automatic continuity and second order cohomology
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 68 / Issue 2 / April 2000
- Published online by Cambridge University Press:
- 09 April 2009, pp. 231-243
- Print publication:
- April 2000
-
- Article
-
- You have access
- Export citation
On topological algebra sheaves
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 61 / Issue 1 / August 1996
- Published online by Cambridge University Press:
- 09 April 2009, pp. 14-29
- Print publication:
- August 1996
-
- Article
-
- You have access
- Export citation
Two commutative amenable non-symmetric Banach algebras
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 59 / Issue 2 / October 1995
- Published online by Cambridge University Press:
- 09 April 2009, pp. 225-231
- Print publication:
- October 1995
-
- Article
-
- You have access
- Export citation
Continuous-trace algebras from the bundle theoretic point of view
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 47 / Issue 3 / December 1989
- Published online by Cambridge University Press:
- 09 April 2009, pp. 368-381
- Print publication:
- December 1989
-
- Article
-
- You have access
- Export citation
On Topological Algebra Bundles
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 43 / Issue 3 / December 1987
- Published online by Cambridge University Press:
- 09 April 2009, pp. 398-419
- Print publication:
- December 1987
-
- Article
-
- You have access
- Export citation
On ext(G2)
- Part of
-
- Journal:
- Mathematika / Volume 28 / Issue 1 / June 1981
- Published online by Cambridge University Press:
- 26 February 2010, pp. 79-85
- Print publication:
- June 1981
-
- Article
- Export citation
Dual functors and the Radon-Nikodym property in the category of Banach spaces
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics / Volume 27 / Issue 4 / June 1979
- Published online by Cambridge University Press:
- 09 April 2009, pp. 479-494
- Print publication:
- June 1979
-
- Article
-
- You have access
- Export citation
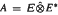 , where
, where 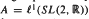 . An important rôle is played by the second Hochschild cohomology group of
. An important rôle is played by the second Hochschild cohomology group of 