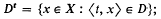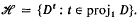Refine listing
Actions for selected content:
126 results in 54Hxx
Lattices of zero-sets
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics / Volume 25 / Issue 2 / March 1978
- Published online by Cambridge University Press:
- 09 April 2009, pp. 189-194
- Print publication:
- March 1978
-
- Article
-
- You have access
- Export citation
Semigroups over generalized trees
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics / Volume 25 / Issue 2 / March 1978
- Published online by Cambridge University Press:
- 09 April 2009, pp. 177-188
- Print publication:
- March 1978
-
- Article
-
- You have access
- Export citation
Generation of σ-algebras, Baire sets and descriptive Borel sets
- Part of
-
- Journal:
- Mathematika / Volume 24 / Issue 2 / December 1977
- Published online by Cambridge University Press:
- 26 February 2010, pp. 241-256
- Print publication:
- December 1977
-
- Article
- Export citation
K-analytic spaces with metrizable compacta
- Part of
-
- Journal:
- Mathematika / Volume 24 / Issue 2 / December 1977
- Published online by Cambridge University Press:
- 26 February 2010, pp. 257-261
- Print publication:
- December 1977
-
- Article
- Export citation
Theorems of Novikov type
- Part of
-
- Journal:
- Mathematika / Volume 24 / Issue 1 / June 1977
- Published online by Cambridge University Press:
- 26 February 2010, pp. 97-114
- Print publication:
- June 1977
-
- Article
- Export citation
Families of compact sets and their universals
- Part of
-
- Journal:
- Mathematika / Volume 21 / Issue 1 / June 1974
- Published online by Cambridge University Press:
- 26 February 2010, pp. 116-127
- Print publication:
- June 1974
-
- Article
- Export citation
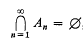
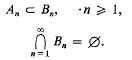
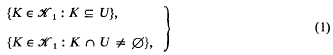
 we shall be concerned with sets in [0, 1] ×
we shall be concerned with sets in [0, 1] ×