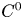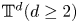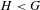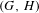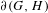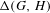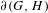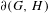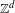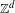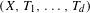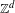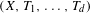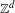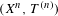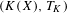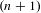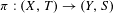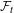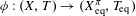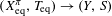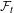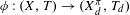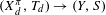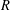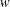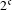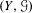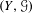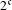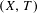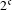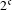Refine listing
Actions for selected content:
126 results in 54Hxx
Continuous flows generate few homeomorphisms
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 63 / Issue 4 / November 2020
- Published online by Cambridge University Press:
- 25 August 2020, pp. 971-983
-
- Article
- Export citation
THE COMPLEXITY OF HOMEOMORPHISM RELATIONS ON SOME CLASSES OF COMPACTA
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 85 / Issue 2 / June 2020
- Published online by Cambridge University Press:
- 18 June 2020, pp. 733-748
- Print publication:
- June 2020
-
- Article
- Export citation
Maximally highly proximal flows
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 7 / July 2021
- Published online by Cambridge University Press:
- 18 May 2020, pp. 2220-2240
- Print publication:
- July 2021
-
- Article
- Export citation
AN APPLICATION OF RECURSION THEORY TO ANALYSIS
- Part of
-
- Journal:
- Bulletin of Symbolic Logic / Volume 26 / Issue 1 / March 2020
- Published online by Cambridge University Press:
- 11 June 2020, pp. 15-25
- Print publication:
- March 2020
-
- Article
- Export citation
Furstenberg boundaries for pairs of groups
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 5 / May 2021
- Published online by Cambridge University Press:
- 20 February 2020, pp. 1514-1529
- Print publication:
- May 2021
-
- Article
- Export citation
Topological mixing of Weyl chamber flows
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 5 / May 2021
- Published online by Cambridge University Press:
- 17 February 2020, pp. 1342-1368
- Print publication:
- May 2021
-
- Article
- Export citation
On the virtual automorphism group of a minimal flow
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 5 / May 2021
- Published online by Cambridge University Press:
- 07 February 2020, pp. 1281-1295
- Print publication:
- May 2021
-
- Article
- Export citation
The Ellis semigroup of certain constant-length substitutions
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 3 / March 2021
- Published online by Cambridge University Press:
- 06 December 2019, pp. 935-960
- Print publication:
- March 2021
-
- Article
- Export citation
There are no proper topological hyperbolic homoclinic classes for area-preserving maps
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 63 / Issue 1 / February 2020
- Published online by Cambridge University Press:
- 12 November 2019, pp. 217-228
-
- Article
- Export citation
Directional dynamical cubes for minimal
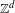 $\mathbb{Z}^{d}$-systems
$\mathbb{Z}^{d}$-systems
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 40 / Issue 12 / December 2020
- Published online by Cambridge University Press:
- 26 June 2019, pp. 3257-3295
- Print publication:
- December 2020
-
- Article
- Export citation
Null systems in the non-minimal case
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 40 / Issue 12 / December 2020
- Published online by Cambridge University Press:
- 17 June 2019, pp. 3420-3437
- Print publication:
- December 2020
-
- Article
- Export citation
The Hausdorff dimension of multiply Xiong chaotic sets
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 40 / Issue 11 / November 2020
- Published online by Cambridge University Press:
- 06 June 2019, pp. 3056-3077
- Print publication:
- November 2020
-
- Article
- Export citation
An answer to Furstenberg’s problem on topological disjointness
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 40 / Issue 9 / September 2020
- Published online by Cambridge University Press:
- 10 April 2019, pp. 2467-2481
- Print publication:
- September 2020
-
- Article
- Export citation
On nilspace systems and their morphisms
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 40 / Issue 11 / November 2020
- Published online by Cambridge University Press:
- 10 April 2019, pp. 3015-3029
- Print publication:
- November 2020
-
- Article
- Export citation
Actions of Semitopological Groups
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 62 / Issue 2 / June 2019
- Published online by Cambridge University Press:
- 04 January 2019, pp. 441-450
- Print publication:
- June 2019
-
- Article
-
- You have access
- Export citation
Relativization of sensitivity in minimal systems
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 40 / Issue 6 / June 2020
- Published online by Cambridge University Press:
- 27 December 2018, pp. 1715-1728
- Print publication:
- June 2020
-
- Article
- Export citation
BEST PROXIMITY POINTS AND FIXED POINTS WITH
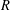 $R$-FUNCTIONS IN THE FRAMEWORK OF
$R$-FUNCTIONS IN THE FRAMEWORK OF 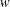 $w$-DISTANCES
$w$-DISTANCES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 99 / Issue 3 / June 2019
- Published online by Cambridge University Press:
- 17 December 2018, pp. 497-507
- Print publication:
- June 2019
-
- Article
-
- You have access
- Export citation
Amenability and unique ergodicity of automorphism groups of countable homogeneous directed graphs
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 40 / Issue 5 / May 2020
- Published online by Cambridge University Press:
- 17 October 2018, pp. 1351-1401
- Print publication:
- May 2020
-
- Article
- Export citation
ON GENERALISED METRISABILITY AND CARDINAL INVARIANTS IN QUASITOPOLOGICAL GROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 99 / Issue 2 / April 2019
- Published online by Cambridge University Press:
- 17 October 2018, pp. 302-310
- Print publication:
- April 2019
-
- Article
-
- You have access
- Export citation
A metric minimal PI cascade with
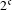 $2^{\mathfrak{c}}$minimal ideals
$2^{\mathfrak{c}}$minimal ideals
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 40 / Issue 5 / May 2020
- Published online by Cambridge University Press:
- 14 September 2018, pp. 1268-1281
- Print publication:
- May 2020
-
- Article
- Export citation