§1. Introduction. In this note we shall discuss a certain dichotomy concerning the pointwise convergence of sequences of analytic sets in completely metrizable separable spaces (Proposition 2.1). The dichotomy is closely related to some reasoning due to W. Szlenk [Sz]; we comment on this in Section 5.1.

In this paper, we obtain the projective cover of the orbit space X/G in terms of the orbit space of the projective space of X, when X is a Tychonoff G-space and G is a finite discrete group. An example shows that finiteness of G is needed.

Topologise the set of continuous self-mappings of a Hausdorff space by the graph topology. When the set of closed subsets of the space is given the upper semi-finite topology then the function which assigns to a map its fixed-point set is continuous. In many familiar cases this is the largest such topology. Related results also hold for the function which assigns to each pair of maps their coincidence set.

Let f be an expansive homeomorphism with the pseudo orbits tracing property on a compact metric space. There are stable and unstable “manifolds” with similar properties as in the hyperbolic case, and similar behavior near periodic points is observed. Per (f) = Ω(f) = CR(f). Mappings Ω and CR are continuous at f.

Some results on fixed points of asymptotically regular mappings are obtained in complete metric spaces and normed linear spaces.

The structure of the set of common fixed points is also discussed in Banach spaces. Our work generalizes essentially known results of Das and Naik, Fisher, Jaggi, Jungck, Rhoades, Singh and Tiwari and several others.

The purpose of this paper is to give some natural examples of Borel-inseparable pairs of coanalytic sets in Polish spaces.

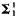A Polish space is a topological space homeomorphic to a separable complete metric space. In this paper, all spaces are uncountable Polish spaces. A pointset is analytic (or ) if it is the continuous image of a Borel set (in any space), or equivalently, the projection of a Borel set, and is 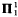coanalytic (or ) if it is the complement of an analytic set. The class of analytic sets is closed under countable unions and intersections, images and preimages by Borel measurable functions, and projections; it is not closed under complements, hence there is an analytic set which is not Borel.

Bassed on the intrinsic structure of a selfmapping T: S → S of an arbitrary set S, called the orbit-structure of T, a new entropy is defined. The idea is to use the number of preimages of an element x under the iterates of T to characterize the complexity of the transformation T and their orbit graphs. The fundamental properties of the orbit entropy related to iteration, iterative roots and iteration semigroups are studied. For continuous (differentiable) functions of Rn to Rn, the chaos of Li and Yorke is characterized by means of this entropy, mainly using the method of Straffingraphs.

Let σ be an ergodic endomorphism of the r–dimensional torus and Π a semigroup generated by two affine transformations lying above σ. We show that the flow defined by Π admits minimal sets of positive Hausdorff dimension and we give necessary and sufficient conditions for this flow to be minimal.

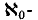In [5] we have developed part of a theory of K- analytic sets that forms a common generalization of the theory of Lindelöf K- analytic sets developed by Choquet, Sion and Frolik and the theory of metric analytic sets developed by Stone and Hansell. As we explain in [5], this theory parallels the recently developed theory of Frolík and Holický, but has certain advantages. In this paper we take the theory rather further, and, in particular, we prove a number of variants of Lusin's first separation theorem and give some of their applications. We make free use of the definitions, notation and conventions introduced in [5].

A maximality principle on quasi-ordered pseudo-metric spaces is used to obtain a number of Lipschitz attraction results for non-semigroup evolution processes with respect to time-dependent families. As particular cases, a multivalued version of Dieudonné's means value theorem and the Kirk-Ray lipschitzianness test are derived.

J. B. Diaz and F. T. Metcalf established some results concerning the structure of the set of cluster points of a sequence of iterates of a continuous self-map of a metric space. In this paper it is shown that their conclusions remain valid if the distance function in their inequality is replaced by a continuous function on the product space. Then this idea is extended to some other mappings and to uniform and general topological spaces.

We state some definitions belonging to the two halves of the title, going far enough to state our main results.

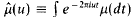Fourier transforms. Let μ be a finite, complex-valued measure on R and its Fourier-Stieltjes transform. We define ℛ to be the set of μ with 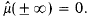When μ ∈ ℛ and φ is of class 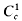(continuously differentiable of compact support), the identity 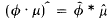shows that θ · μ ∈ ℛ.

Some results on fixed points of certain involutions in Banach spaces have been obtained, and whence a few coincidence theorems are also derived. These are indeed generalization of previously known results due to Browder, Goebel-Zlotkiewicz and Iséki. Illustrative examples are also given.

In [4] we initiated a study of K-Lusin sets. We characterized the K-Lusin sets in a Hausdorff space X as the sets that can be obtained as the image of some paracompact Čech complete space G, under a continuous injective map that maps discrete families in G to discretely σ-decomposable families in X [4, Theorem 2, p. 195]. Unfortunately, we cannot substantiate a second characterization of K-Lusin sets in completely regular spaces, given in the second part of Theorem 14 of [4].

The classical theory of analytic sets works well in metric spaces, but the analytic sets themselves are automatically separable. The theory of K-analytic sets, developed by Choquet, Sion, Frolik and others, works well in Hausdorff spaces, but the K-analytic sets themselves remain Lindelof. The theory of k-analytic sets developed by A. H. Stone and R. W. Hansell works well in non-separable metric spaces, especially in the special case, when k is ℵ0, with which we shall be concerned, see [9, 10 and 16–20]. Of course the k-analytic sets are metrizable. For accounts of these theories, see, for example, [15].

Every poset with 0 is determined by various semigroups of isotone selfmaps which preserve 0. Two theorems along these lines are given and applied to some recent results concerning relation semigroups on topological spaces.

Reduced rings and lattice-ordered groups are examples of groups with Boolean orthogonalities. In this note we show that any group with a Boolean orthogonality satisfying a finiteness condition introduced by Stewart is isomorphic with a group of homeomorphisms of a topological space, in which two homeomorphisms are orthogonal if and only if they have disjoint supports.

This second part follows on directly from the first part that appears on pages 125–156 of this volume. The references for this part are included amongst the references appearing at the end of the first part.

A Borel isomorphism that, together with its inverse, maps ℱσ-sets to ℱσ-sets will be said to be a Borel isomorphism at the first level. Such a Borel isomorphism will be called a first level isomorphism, for short. We study such first level isomorphisms between Polish spaces and between their Borel and analytic subsets.

Some fixed point theorems are obtained for weekly inward mappings which extend or generalize those results by K. Fan, B. Halpern or S. Reich. Various formulations of inward and outward concepts are also briefly discussed.