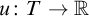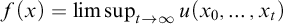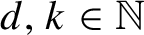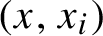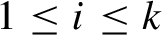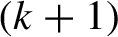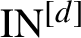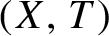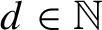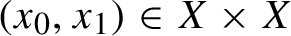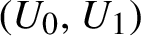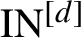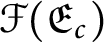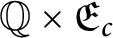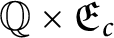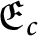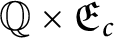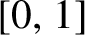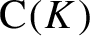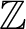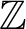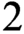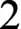Refine listing
Actions for selected content:
126 results in 54Hxx
Point Degree Spectra of Represented Spaces
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 10 / 2022
- Published online by Cambridge University Press:
- 27 May 2022, e31
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Invariant Ideal Axiom
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 10 / 2022
- Published online by Cambridge University Press:
- 20 May 2022, e29
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
GAMES CHARACTERIZING LIMSUP FUNCTIONS AND BAIRE CLASS 1 FUNCTIONS
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 87 / Issue 4 / December 2022
- Published online by Cambridge University Press:
- 13 April 2022, pp. 1459-1473
- Print publication:
- December 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
FORCING CONSTRUCTIONS AND COUNTABLE BOREL EQUIVALENCE RELATIONS
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 87 / Issue 3 / September 2022
- Published online by Cambridge University Press:
- 14 March 2022, pp. 873-893
- Print publication:
- September 2022
-
- Article
- Export citation
The spectrum of a localic semiring
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 173 / Issue 3 / November 2022
- Published online by Cambridge University Press:
- 28 February 2022, pp. 647-668
- Print publication:
- November 2022
-
- Article
- Export citation
Independence and almost automorphy of higher order
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 43 / Issue 4 / April 2023
- Published online by Cambridge University Press:
- 18 February 2022, pp. 1363-1381
- Print publication:
- April 2023
-
- Article
-
- You have access
- HTML
- Export citation
BOHR COMPACTIFICATIONS OF GROUPS AND RINGS
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 88 / Issue 3 / September 2023
- Published online by Cambridge University Press:
- 04 February 2022, pp. 1103-1137
- Print publication:
- September 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A characterization of the product of the rational numbers and complete Erdős space
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 1 / March 2023
- Published online by Cambridge University Press:
- 27 January 2022, pp. 87-102
- Print publication:
- March 2023
-
- Article
- Export citation
CONSTRUCTING WADGE CLASSES
- Part of
-
- Journal:
- Bulletin of Symbolic Logic / Volume 28 / Issue 2 / June 2022
- Published online by Cambridge University Press:
- 26 January 2022, pp. 207-257
- Print publication:
- June 2022
-
- Article
- Export citation
Chief factors in Polish groups
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 173 / Issue 2 / September 2022
- Published online by Cambridge University Press:
- 30 June 2021, pp. 239-296
- Print publication:
- September 2022
-
- Article
- Export citation
On topological rank of factors of Cantor minimal systems
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 42 / Issue 9 / September 2022
- Published online by Cambridge University Press:
- 08 June 2021, pp. 2866-2889
- Print publication:
- September 2022
-
- Article
- Export citation
AUTOMATIC CONTINUITY FOR ISOMETRY GROUPS – ERRATUM
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 21 / Issue 6 / November 2022
- Published online by Cambridge University Press:
- 02 February 2021, pp. 2253-2255
- Print publication:
- November 2022
-
- Article
- Export citation
ON THE AUTOMORPHISM GROUP OF THE UNIVERSAL HOMOGENEOUS MEET-TREE
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 86 / Issue 4 / December 2021
- Published online by Cambridge University Press:
- 01 February 2021, pp. 1508-1540
- Print publication:
- December 2021
-
- Article
- Export citation
On Polish groups admitting non-essentially countable actions
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 42 / Issue 1 / January 2022
- Published online by Cambridge University Press:
- 29 December 2020, pp. 180-194
- Print publication:
- January 2022
-
- Article
-
- You have access
- Open access
- Export citation
Generic homeomorphisms have full metric mean dimension
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 42 / Issue 1 / January 2022
- Published online by Cambridge University Press:
- 28 December 2020, pp. 40-64
- Print publication:
- January 2022
-
- Article
- Export citation
Expansive dynamics on locally compact groups
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 12 / December 2021
- Published online by Cambridge University Press:
- 18 November 2020, pp. 3768-3779
- Print publication:
- December 2021
-
- Article
- Export citation
On equicontinuous factors of flows on locally path-connected compact spaces
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 11 / November 2021
- Published online by Cambridge University Press:
- 13 November 2020, pp. 3270-3287
- Print publication:
- November 2021
-
- Article
- Export citation
Complete regularity of Ellis semigroups of
 $\mathbb{Z} $-actions
$\mathbb{Z} $-actions
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 12 / December 2021
- Published online by Cambridge University Press:
- 13 November 2020, pp. 3593-3609
- Print publication:
- December 2021
-
- Article
- Export citation
DECOMPOSING FUNCTIONS OF BAIRE CLASS
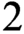 $2$ ON POLISH SPACES
$2$ ON POLISH SPACES
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 85 / Issue 3 / September 2020
- Published online by Cambridge University Press:
- 26 October 2020, pp. 960-971
- Print publication:
- September 2020
-
- Article
- Export citation
BASES FOR FUNCTIONS BEYOND THE FIRST BAIRE CLASS
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 85 / Issue 3 / September 2020
- Published online by Cambridge University Press:
- 27 October 2020, pp. 1289-1303
- Print publication:
- September 2020
-
- Article
- Export citation