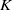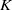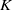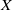Refine listing
Actions for selected content:
126 results in 54Hxx
On Følner sets in topological groups
- Part of
-
- Journal:
- Compositio Mathematica / Volume 154 / Issue 7 / July 2018
- Published online by Cambridge University Press:
- 16 May 2018, pp. 1333-1361
- Print publication:
- July 2018
-
- Article
- Export citation
Diffeomorphism groups of tame Cantor sets and Thompson-like groups
- Part of
-
- Journal:
- Compositio Mathematica / Volume 154 / Issue 5 / May 2018
- Published online by Cambridge University Press:
- 03 April 2018, pp. 1066-1110
- Print publication:
- May 2018
-
- Article
- Export citation
LYAPUNOV EXPONENTS ON METRIC SPACES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 97 / Issue 1 / February 2018
- Published online by Cambridge University Press:
- 04 October 2017, pp. 153-162
- Print publication:
- February 2018
-
- Article
-
- You have access
- Export citation
AUTOMATIC CONTINUITY FOR ISOMETRY GROUPS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 18 / Issue 3 / May 2019
- Published online by Cambridge University Press:
- 11 April 2017, pp. 561-590
- Print publication:
- May 2019
-
- Article
- Export citation
TWO-SIDED SHIFT SPACES OVER INFINITE ALPHABETS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 103 / Issue 3 / December 2017
- Published online by Cambridge University Press:
- 22 March 2017, pp. 357-386
- Print publication:
- December 2017
-
- Article
-
- You have access
- Export citation
COMPACT SPACES OF THE FIRST BAIRE CLASS THAT HAVE OPEN FINITE DEGREE
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 17 / Issue 5 / November 2018
- Published online by Cambridge University Press:
- 21 November 2016, pp. 1173-1196
- Print publication:
- November 2018
-
- Article
- Export citation
ON VARIETIES OF ABELIAN TOPOLOGICAL GROUPS WITH COPRODUCTS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 95 / Issue 1 / February 2017
- Published online by Cambridge University Press:
- 19 October 2016, pp. 54-65
- Print publication:
- February 2017
-
- Article
-
- You have access
- Export citation
BEST PROXIMITY POINT THEOREMS FOR CYCLIC QUASI-CONTRACTION MAPS IN UNIFORMLY CONVEX BANACH SPACES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 95 / Issue 1 / February 2017
- Published online by Cambridge University Press:
- 13 October 2016, pp. 149-156
- Print publication:
- February 2017
-
- Article
-
- You have access
- Export citation
FIXED POINTS THEOREMS FOR GENERALISED WEAKLY CONTRACTIVE MAPPINGS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 93 / Issue 2 / April 2016
- Published online by Cambridge University Press:
- 04 September 2015, pp. 321-329
- Print publication:
- April 2016
-
- Article
-
- You have access
- Export citation
NOTES ON
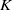 $K$-TOPOLOGICAL GROUPS AND HOMEOMORPHISMS OF TOPOLOGICAL GROUPS
$K$-TOPOLOGICAL GROUPS AND HOMEOMORPHISMS OF TOPOLOGICAL GROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 87 / Issue 3 / June 2013
- Published online by Cambridge University Press:
- 30 August 2012, pp. 493-502
- Print publication:
- June 2013
-
- Article
-
- You have access
- Export citation
ON DENSE EMBEDDINGS INTO MOORE SPACES WITH THE BAIRE PROPERTY
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 83 / Issue 1 / February 2011
- Published online by Cambridge University Press:
- 29 October 2010, pp. 1-10
- Print publication:
- February 2011
-
- Article
-
- You have access
- Export citation
Étale groupoids as germ groupoids and their base extensions
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 53 / Issue 3 / October 2010
- Published online by Cambridge University Press:
- 05 August 2010, pp. 765-785
-
- Article
-
- You have access
- Export citation
THE FATOU COMPLETION OF A FRÉCHET FUNCTION SPACE AND APPLICATIONS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 88 / Issue 1 / February 2010
- Published online by Cambridge University Press:
- 08 December 2009, pp. 49-60
- Print publication:
- February 2010
-
- Article
-
- You have access
- Export citation
ON FIXED POINTS OF GENERALIZED SET-VALUED CONTRACTIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 81 / Issue 1 / February 2010
- Published online by Cambridge University Press:
- 23 July 2009, pp. 16-22
- Print publication:
- February 2010
-
- Article
-
- You have access
- Export citation
WEAK CONVERGENCE OF AN ITERATIVE SCHEME FOR GENERALIZED EQUILIBRIUM PROBLEMS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 79 / Issue 3 / June 2009
- Published online by Cambridge University Press:
- 05 May 2009, pp. 437-453
- Print publication:
- June 2009
-
- Article
-
- You have access
- Export citation
CONTINUOUS AND DISCRETE FLOWS ON OPERATOR ALGEBRAS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 86 / Issue 2 / April 2009
- Published online by Cambridge University Press:
- 01 April 2009, pp. 169-176
- Print publication:
- April 2009
-
- Article
-
- You have access
- Export citation
A WEAKLY ANALYTIC LOCALLY CONVEX SPACE WHICH IS NOT K-ANALYTIC
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 79 / Issue 1 / February 2009
- Published online by Cambridge University Press:
- 09 February 2009, pp. 31-35
- Print publication:
- February 2009
-
- Article
-
- You have access
- Export citation
CONTINUITY OF MEASURABLE HOMOMORPHISMS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 78 / Issue 1 / August 2008
- Published online by Cambridge University Press:
- 01 August 2008, pp. 171-176
- Print publication:
- August 2008
-
- Article
-
- You have access
- Export citation
A NOTE ON SPACES Cp(X)K-ANALYTIC-FRAMED IN ℝX
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 78 / Issue 1 / August 2008
- Published online by Cambridge University Press:
- 01 August 2008, pp. 141-146
- Print publication:
- August 2008
-
- Article
-
- You have access
- Export citation
ON THE FUNDAMENTAL REGIONS OF A FIXED POINT FREE CONSERVATIVE HÉNON MAP
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 77 / Issue 1 / February 2008
- Published online by Cambridge University Press:
- 01 February 2008, pp. 37-48
- Print publication:
- February 2008
-
- Article
-
- You have access
- Export citation