Refine listing
Actions for selected content:
27 results in 19Kxx
Positive Curvature, Partial Vanishing Theorems and Coarse Indices
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 59 / Issue 1 / February 2016
- Published online by Cambridge University Press:
- 22 July 2015, pp. 223-233
-
- Article
- Export citation
Classifying Polygonal Algebras by their K0-Group
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 58 / Issue 2 / June 2015
- Published online by Cambridge University Press:
- 13 February 2015, pp. 485-497
-
- Article
-
- You have access
- Export citation
Box splines and the equivariant index theorem
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 12 / Issue 3 / July 2013
- Published online by Cambridge University Press:
- 01 June 2012, pp. 503-544
- Print publication:
- July 2013
-
- Article
- Export citation
Morita equivalences and KK-theory for Banach algebras
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 8 / Issue 3 / July 2009
- Published online by Cambridge University Press:
- 15 December 2008, pp. 565-593
- Print publication:
- July 2009
-
- Article
- Export citation
Equivariant KK-theory for inverse limits of G-C*-algebras
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 56 / Issue 2 / April 1994
- Published online by Cambridge University Press:
- 09 April 2009, pp. 183-211
- Print publication:
- April 1994
-
- Article
-
- You have access
- Export citation
The Toeplitz operator proof of noncommutative Bott periodicity
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 53 / Issue 2 / October 1992
- Published online by Cambridge University Press:
- 09 April 2009, pp. 229-251
- Print publication:
- October 1992
-
- Article
-
- You have access
- Export citation
Continuous-trace algebras from the bundle theoretic point of view
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 47 / Issue 3 / December 1989
- Published online by Cambridge University Press:
- 09 April 2009, pp. 368-381
- Print publication:
- December 1989
-
- Article
-
- You have access
- Export citation
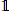 of the identity in
of the identity in 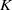
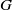
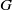
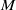
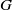
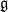
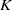
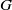
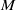
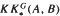 are extended to the setting of inverse limits of
are extended to the setting of inverse limits of 