Refine listing
Actions for selected content:
27 results in 19Kxx
KK-theory of circle actions with the Rokhlin property
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 14 February 2025, pp. 1-29
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Generalised Dirac-Schrödinger operators and the Callias Theorem
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 24 January 2025, e11
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
RANKS OF SOFT OPERATORS IN NOWHERE SCATTERED
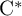 $\mathrm {C}^*$-ALGEBRAS
$\mathrm {C}^*$-ALGEBRAS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 24 / Issue 2 / March 2025
- Published online by Cambridge University Press:
- 20 December 2024, pp. 371-410
- Print publication:
- March 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A CATEGORICAL APPROACH TO THE BAUM–CONNES CONJECTURE FOR ÉTALE GROUPOIDS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 23 / Issue 5 / September 2024
- Published online by Cambridge University Press:
- 02 January 2024, pp. 2319-2364
- Print publication:
- September 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Homology and K-theory of dynamical systems I. Torsion-free ample groupoids
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 42 / Issue 8 / August 2022
- Published online by Cambridge University Press:
- 04 June 2021, pp. 2630-2660
- Print publication:
- August 2022
-
- Article
- Export citation
The Cuntz semigroup and the radius of comparison of the crossed product by a finite group
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 12 / December 2021
- Published online by Cambridge University Press:
- 10 March 2021, pp. 3541-3592
- Print publication:
- December 2021
-
- Article
- Export citation
Deformation of Dirac operators along orbits and quantization of noncompact Hamiltonian torus manifolds
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 74 / Issue 4 / August 2022
- Published online by Cambridge University Press:
- 09 March 2021, pp. 1062-1092
- Print publication:
- August 2022
-
- Article
- Export citation
The Baum–Connes conjecture localised at the unit element of a discrete group
- Part of
-
- Journal:
- Compositio Mathematica / Volume 156 / Issue 12 / December 2020
- Published online by Cambridge University Press:
- 14 January 2021, pp. 2536-2559
- Print publication:
- December 2020
-
- Article
- Export citation
DIRAC OPERATORS ON ORIENTIFOLDS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 104 / Issue 1 / August 2021
- Published online by Cambridge University Press:
- 30 October 2020, pp. 167-168
- Print publication:
- August 2021
-
- Article
-
- You have access
- Export citation
Edwards' condition for quasitraces on C*-algebras
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 151 / Issue 2 / April 2021
- Published online by Cambridge University Press:
- 08 April 2020, pp. 525-547
- Print publication:
- April 2021
-
- Article
-
- You have access
- Open access
- Export citation
The Category of Ordered Bratteli Diagrams
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 73 / Issue 1 / February 2021
- Published online by Cambridge University Press:
- 03 September 2019, pp. 1-28
- Print publication:
- February 2021
-
- Article
- Export citation
EQUIVARIANT ALGEBRAIC INDEX THEOREM
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 20 / Issue 3 / May 2021
- Published online by Cambridge University Press:
- 27 August 2019, pp. 929-955
- Print publication:
- May 2021
-
- Article
- Export citation
POSITIVE SCALAR CURVATURE AND CALLIAS-TYPE INDEX THEOREMS FOR PROPER ACTIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 99 / Issue 2 / April 2019
- Published online by Cambridge University Press:
- 07 January 2019, pp. 342-343
- Print publication:
- April 2019
-
- Article
-
- You have access
- Export citation
Spectral Flow Argument Localizing an Odd Index Pairing
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 62 / Issue 2 / June 2019
- Published online by Cambridge University Press:
- 07 January 2019, pp. 373-381
- Print publication:
- June 2019
-
- Article
-
- You have access
- Export citation
Integral Formula for Spectral Flow for
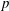 $p$-Summable Operators
$p$-Summable Operators
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 71 / Issue 2 / April 2019
- Published online by Cambridge University Press:
- 07 January 2019, pp. 337-379
- Print publication:
- April 2019
-
- Article
-
- You have access
- Export citation
FACTORISATION OF EQUIVARIANT SPECTRAL TRIPLES IN UNBOUNDED
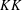 $KK$-THEORY
$KK$-THEORY
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 107 / Issue 2 / October 2019
- Published online by Cambridge University Press:
- 21 December 2018, pp. 145-180
- Print publication:
- October 2019
-
- Article
-
- You have access
- Export citation
Perforation conditions and almost algebraic order in Cuntz semigroups
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 148 / Issue 4 / August 2018
- Published online by Cambridge University Press:
- 18 April 2018, pp. 669-702
- Print publication:
- August 2018
-
- Article
- Export citation
An Equivariant Theory for the Bivariant Cuntz Semigroup
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 61 / Issue 2 / May 2018
- Published online by Cambridge University Press:
- 04 April 2018, pp. 573-598
-
- Article
- Export citation
TOPOLOGICAL STATES OF MATTER AND NONCOMMUTATIVE GEOMETRY
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 94 / Issue 2 / October 2016
- Published online by Cambridge University Press:
- 21 July 2016, p. 349
- Print publication:
- October 2016
-
- Article
-
- You have access
- Export citation
LORENTZIAN GEOMETRY AND PHYSICS IN KASPAROV’S THEORY
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 93 / Issue 2 / April 2016
- Published online by Cambridge University Press:
- 21 January 2016, pp. 340-341
- Print publication:
- April 2016
-
- Article
-
- You have access
- Export citation
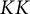
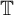
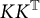
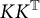

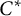
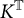
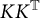
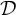
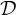
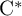
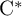
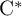
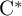
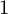
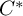

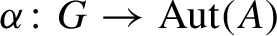
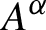
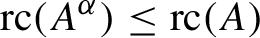
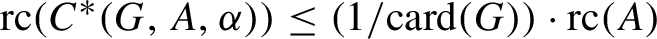
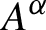
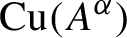
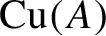
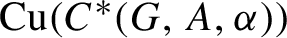
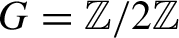
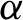
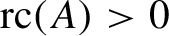
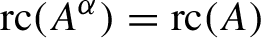
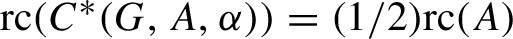
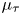
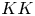
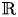
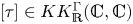
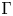
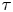
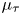
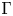


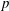
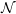

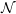
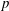
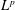
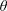
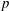
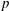
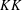
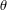
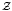 ) in terms of Cu(
) in terms of Cu(