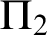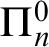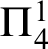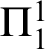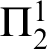Refine listing
Actions for selected content:
166 results in 03FXX
RUSSELLIAN DEFINITE DESCRIPTION THEORY—A PROOF THEORETIC APPROACH
- Part of
-
- Journal:
- The Review of Symbolic Logic / Volume 16 / Issue 2 / June 2023
- Published online by Cambridge University Press:
- 02 July 2021, pp. 624-649
- Print publication:
- June 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
SUBATOMIC INFERENCES: AN INFERENTIALIST SEMANTICS FOR ATOMICS, PREDICATES, AND NAMES
- Part of
-
- Journal:
- The Review of Symbolic Logic / Volume 16 / Issue 3 / September 2023
- Published online by Cambridge University Press:
- 02 July 2021, pp. 672-699
- Print publication:
- September 2023
-
- Article
- Export citation
PRENEX NORMAL FORM THEOREMS IN SEMI-CLASSICAL ARITHMETIC
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 86 / Issue 3 / September 2021
- Published online by Cambridge University Press:
- 11 June 2021, pp. 1124-1153
- Print publication:
- September 2021
-
- Article
- Export citation
MÜNCHHAUSEN PROVABILITY
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 86 / Issue 3 / September 2021
- Published online by Cambridge University Press:
- 10 June 2021, pp. 1006-1034
- Print publication:
- September 2021
-
- Article
- Export citation
GOODSTEIN SEQUENCES BASED ON A PARAMETRIZED ACKERMANN–PÉTER FUNCTION
- Part of
-
- Journal:
- Bulletin of Symbolic Logic / Volume 27 / Issue 2 / June 2021
- Published online by Cambridge University Press:
- 02 July 2021, pp. 168-186
- Print publication:
- June 2021
-
- Article
- Export citation
BOUNDED-ANALYTIC SEQUENT CALCULI AND EMBEDDINGS FOR HYPERSEQUENT LOGICS
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 86 / Issue 2 / June 2021
- Published online by Cambridge University Press:
- 11 June 2021, pp. 635-668
- Print publication:
- June 2021
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
THE NONARITHMETICITY OF THE PREDICATE LOGIC OF STRICTLY PRIMITIVE RECURSIVE REALIZABILITY
- Part of
-
- Journal:
- The Review of Symbolic Logic / Volume 15 / Issue 3 / September 2022
- Published online by Cambridge University Press:
- 19 April 2021, pp. 693-721
- Print publication:
- September 2022
-
- Article
- Export citation
TRANSLATIONS BETWEEN LINEAR AND TREE NATURAL DEDUCTION SYSTEMS FOR RELEVANT LOGICS
- Part of
-
- Journal:
- The Review of Symbolic Logic / Volume 14 / Issue 2 / June 2021
- Published online by Cambridge University Press:
- 08 April 2021, pp. 285-306
- Print publication:
- June 2021
-
- Article
- Export citation
NONCLASSICAL TRUTH WITH CLASSICAL STRENGTH. A PROOF-THEORETIC ANALYSIS OF COMPOSITIONAL TRUTH OVER HYPE
- Part of
-
- Journal:
- The Review of Symbolic Logic / Volume 16 / Issue 2 / June 2023
- Published online by Cambridge University Press:
- 25 March 2021, pp. 425-448
- Print publication:
- June 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ABSTRACT FORMS OF QUANTIFICATION IN THE QUANTIFIED ARGUMENT CALCULUS
- Part of
-
- Journal:
- The Review of Symbolic Logic / Volume 16 / Issue 2 / June 2023
- Published online by Cambridge University Press:
- 08 March 2021, pp. 449-479
- Print publication:
- June 2023
-
- Article
- Export citation
FREGE’S THEORY OF REAL NUMBERS: A CONSISTENT RENDERING
- Part of
-
- Journal:
- The Review of Symbolic Logic / Volume 15 / Issue 3 / September 2022
- Published online by Cambridge University Press:
- 22 February 2021, pp. 624-667
- Print publication:
- September 2022
-
- Article
- Export citation
WELL ORDERING PRINCIPLES AND
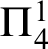 ${\Pi }^{1}_{4}$-STATEMENTS: A PILOT STUDY
${\Pi }^{1}_{4}$-STATEMENTS: A PILOT STUDY
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 86 / Issue 2 / June 2021
- Published online by Cambridge University Press:
- 16 February 2021, pp. 709-745
- Print publication:
- June 2021
-
- Article
- Export citation
A MARRIAGE OF BROUWER’S INTUITIONISM AND HILBERT’S FINITISM I: ARITHMETIC
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 87 / Issue 2 / June 2022
- Published online by Cambridge University Press:
- 07 January 2021, pp. 437-497
- Print publication:
- June 2022
-
- Article
- Export citation
DISJUNCTIONS WITH STOPPING CONDITIONS
- Part of
-
- Journal:
- Bulletin of Symbolic Logic / Volume 27 / Issue 3 / September 2021
- Published online by Cambridge University Press:
- 05 January 2021, pp. 231-253
- Print publication:
- September 2021
-
- Article
- Export citation
CURRENT RESEARCH ON GÖDEL’S INCOMPLETENESS THEOREMS
- Part of
-
- Journal:
- Bulletin of Symbolic Logic / Volume 27 / Issue 2 / June 2021
- Published online by Cambridge University Press:
- 05 January 2021, pp. 113-167
- Print publication:
- June 2021
-
- Article
- Export citation
WHAT IS A RULE OF INFERENCE?
- Part of
-
- Journal:
- The Review of Symbolic Logic / Volume 14 / Issue 2 / June 2021
- Published online by Cambridge University Press:
- 21 December 2020, pp. 307-346
- Print publication:
- June 2021
-
- Article
- Export citation
BOUNDS FOR INDEXES OF NILPOTENCY IN COMMUTATIVE RING THEORY: A PROOF MINING APPROACH
- Part of
-
- Journal:
- Bulletin of Symbolic Logic / Volume 26 / Issue 3-4 / December 2020
- Published online by Cambridge University Press:
- 05 January 2021, pp. 257-267
- Print publication:
- December 2020
-
- Article
- Export citation
LIFSCHITZ REALIZABILITY AS A TOPOLOGICAL CONSTRUCTION
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 85 / Issue 4 / December 2020
- Published online by Cambridge University Press:
- 08 January 2021, pp. 1342-1375
- Print publication:
- December 2020
-
- Article
- Export citation
FINDING THE LIMIT OF INCOMPLETENESS I
- Part of
-
- Journal:
- Bulletin of Symbolic Logic / Volume 26 / Issue 3-4 / December 2020
- Published online by Cambridge University Press:
- 16 April 2021, pp. 268-286
- Print publication:
- December 2020
-
- Article
- Export citation
WEIHRAUCH GOES BROUWERIAN
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 85 / Issue 4 / December 2020
- Published online by Cambridge University Press:
- 30 October 2020, pp. 1614-1653
- Print publication:
- December 2020
-
- Article
- Export citation