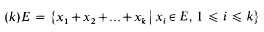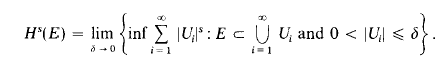Refine listing
Actions for selected content:
354 results in 28Axx
Families of sets on a finite set
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 37 / Issue 3 / December 1984
- Published online by Cambridge University Press:
- 09 April 2009, pp. 405-412
- Print publication:
- December 1984
-
- Article
-
- You have access
- Export citation
An Fσ semigroup of zero measure which contains a translate of every countable set
- Part of
-
- Journal:
- Mathematika / Volume 31 / Issue 2 / December 1984
- Published online by Cambridge University Press:
- 26 February 2010, pp. 272-281
- Print publication:
- December 1984
-
- Article
- Export citation
On translation-bounded measures
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 37 / Issue 1 / August 1984
- Published online by Cambridge University Press:
- 09 April 2009, pp. 139-142
- Print publication:
- August 1984
-
- Article
-
- You have access
- Export citation
Rings of fractional dimension
- Part of
-
- Journal:
- Mathematika / Volume 31 / Issue 1 / June 1984
- Published online by Cambridge University Press:
- 26 February 2010, pp. 25-27
- Print publication:
- June 1984
-
- Article
- Export citation
A very sparse set of dimension 1
- Part of
-
- Journal:
- Mathematika / Volume 31 / Issue 1 / June 1984
- Published online by Cambridge University Press:
- 26 February 2010, pp. 42-46
- Print publication:
- June 1984
-
- Article
- Export citation
A general measure decomposition theorem by means of the generalized wallman remainder
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 36 / Issue 1 / February 1984
- Published online by Cambridge University Press:
- 09 April 2009, pp. 87-105
- Print publication:
- February 1984
-
- Article
-
- You have access
- Export citation
When is the algebra of regular sets for a finitely additive borel measure a α-algebra?
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 33 / Issue 3 / December 1982
- Published online by Cambridge University Press:
- 09 April 2009, pp. 374-385
- Print publication:
- December 1982
-
- Article
-
- You have access
- Export citation
The recognition of certain Hausdorff like measures
- Part of
-
- Journal:
- Mathematika / Volume 29 / Issue 2 / December 1982
- Published online by Cambridge University Press:
- 26 February 2010, pp. 260-263
- Print publication:
- December 1982
-
- Article
- Export citation
Initial and relative limiting behaviour of temperatures on a strip
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 33 / Issue 2 / October 1982
- Published online by Cambridge University Press:
- 09 April 2009, pp. 213-228
- Print publication:
- October 1982
-
- Article
-
- You have access
- Export citation
The existence of locally fine simplicial subdivisions
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 33 / Issue 1 / August 1982
- Published online by Cambridge University Press:
- 09 April 2009, pp. 114-124
- Print publication:
- August 1982
-
- Article
-
- You have access
- Export citation
Hausdorff dimension and the exceptional set of projections
- Part of
-
- Journal:
- Mathematika / Volume 29 / Issue 1 / June 1982
- Published online by Cambridge University Press:
- 26 February 2010, pp. 109-115
- Print publication:
- June 1982
-
- Article
- Export citation
Lifting properties and uniform regularity of lebesgue measures on topological spaces
- Part of
-
- Journal:
- Mathematika / Volume 28 / Issue 2 / December 1981
- Published online by Cambridge University Press:
- 26 February 2010, pp. 198-205
- Print publication:
- December 1981
-
- Article
- Export citation
The necessity of sigma-finiteness in the radon–nikodym theorem
- Part of
-
- Journal:
- Mathematika / Volume 28 / Issue 1 / June 1981
- Published online by Cambridge University Press:
- 26 February 2010, pp. 99-101
- Print publication:
- June 1981
-
- Article
- Export citation
Mesures coniques et intégrale de Daniell
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 31 / Issue 1 / June 1981
- Published online by Cambridge University Press:
- 09 April 2009, pp. 46-58
- Print publication:
- June 1981
-
- Article
-
- You have access
- Export citation
Rarefaction indices
- Part of
-
- Journal:
- Mathematika / Volume 27 / Issue 1 / June 1980
- Published online by Cambridge University Press:
- 26 February 2010, pp. 46-57
- Print publication:
- June 1980
-
- Article
- Export citation
Sections of Sets of zero Lebesgue measure
- Part of
-
- Journal:
- Mathematika / Volume 27 / Issue 1 / June 1980
- Published online by Cambridge University Press:
- 26 February 2010, pp. 90-96
- Print publication:
- June 1980
-
- Article
- Export citation
Uniform boundedness principles for regular Borel vector measures
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 29 / Issue 2 / March 1980
- Published online by Cambridge University Press:
- 09 April 2009, pp. 206-218
- Print publication:
- March 1980
-
- Article
-
- You have access
- Export citation
Packing planes in ℝ3
- Part of
-
- Journal:
- Mathematika / Volume 26 / Issue 2 / December 1979
- Published online by Cambridge University Press:
- 26 February 2010, pp. 180-183
- Print publication:
- December 1979
-
- Article
- Export citation
Measurability of cross section measure of a product Borel set
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics / Volume 28 / Issue 3 / November 1979
- Published online by Cambridge University Press:
- 09 April 2009, pp. 346-352
- Print publication:
- November 1979
-
- Article
-
- You have access
- Export citation
Packing smooth curves in Rq
- Part of
-
- Journal:
- Mathematika / Volume 26 / Issue 1 / June 1979
- Published online by Cambridge University Press:
- 26 February 2010, pp. 1-12
- Print publication:
- June 1979
-
- Article
- Export citation