Refine listing
Actions for selected content:
352 results in 28Axx
POLAR DECOMPOSITION OF THE k-FOLD PRODUCT OF LEBESGUE MEASURE ON ℝn
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 85 / Issue 2 / April 2012
- Published online by Cambridge University Press:
- 06 January 2012, pp. 315-324
- Print publication:
- April 2012
-
- Article
-
- You have access
- Export citation
LEAST SQUARES APPROXIMATIONS OF MEASURES VIA GEOMETRIC CONDITION NUMBERS
- Part of
-
- Journal:
- Mathematika / Volume 58 / Issue 1 / January 2012
- Published online by Cambridge University Press:
- 20 December 2011, pp. 45-70
- Print publication:
- January 2012
-
- Article
- Export citation
TWO NONTRIVIAL WEAK SOLUTIONS FOR THE DIRICHLET PROBLEM ON THE SIERPIŃSKI GASKET
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 85 / Issue 3 / June 2012
- Published online by Cambridge University Press:
- 12 December 2011, pp. 395-414
- Print publication:
- June 2012
-
- Article
-
- You have access
- Export citation
BALANCED CONVEX PARTITIONS OF MEASURES IN ℝd
- Part of
-
- Journal:
- Mathematika / Volume 58 / Issue 1 / January 2012
- Published online by Cambridge University Press:
- 21 October 2011, pp. 71-76
- Print publication:
- January 2012
-
- Article
- Export citation
NOTE ABOUT LINDELÖF Σ-SPACES υX
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 85 / Issue 1 / February 2012
- Published online by Cambridge University Press:
- 28 September 2011, pp. 114-120
- Print publication:
- February 2012
-
- Article
-
- You have access
- Export citation
On Hölder continuity-in-time of the optimal transport map towards measures along a curve
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 54 / Issue 2 / June 2011
- Published online by Cambridge University Press:
- 31 March 2011, pp. 401-409
-
- Article
-
- You have access
- Export citation
Curves of infinite length in labyrinth fractals
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 54 / Issue 2 / June 2011
- Published online by Cambridge University Press:
- 30 March 2011, pp. 329-344
-
- Article
-
- You have access
- Export citation
Multifractal spectra for random self-similar measures via branching processes
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 43 / Issue 1 / March 2011
- Published online by Cambridge University Press:
- 01 July 2016, pp. 1-39
- Print publication:
- March 2011
-
- Article
-
- You have access
- Export citation
SPECTRAL GAP FOR SOME INVARIANT LOG-CONCAVE PROBABILITY MEASURES
- Part of
-
- Journal:
- Mathematika / Volume 57 / Issue 1 / January 2011
- Published online by Cambridge University Press:
- 22 November 2010, pp. 51-62
- Print publication:
- January 2011
-
- Article
- Export citation
The spectra of the Laplacians of fractal graphs not satisfying spectral decimation
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 53 / Issue 3 / October 2010
- Published online by Cambridge University Press:
- 12 August 2010, pp. 731-746
-
- Article
-
- You have access
- Export citation
Upper conical density results for general measures on ℝn
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 53 / Issue 2 / June 2010
- Published online by Cambridge University Press:
- 30 April 2010, pp. 311-331
-
- Article
-
- You have access
- Export citation
Simultaneous Multifractal Analysis of the Branching and Visibility Measure on a Galton-Watson Tree
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 42 / Issue 1 / March 2010
- Published online by Cambridge University Press:
- 01 July 2016, pp. 226-245
- Print publication:
- March 2010
-
- Article
-
- You have access
- Export citation
RANDOM SUBSETS OF SELF-AFFINE FRACTALS
- Part of
-
- Journal:
- Mathematika / Volume 56 / Issue 1 / January 2010
- Published online by Cambridge University Press:
- 10 December 2009, pp. 61-76
- Print publication:
- January 2010
-
- Article
- Export citation
PRODUCT FRACTAL SETS DETERMINED BY STABLE PROCESSES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 79 / Issue 2 / April 2009
- Published online by Cambridge University Press:
- 26 February 2009, pp. 201-212
- Print publication:
- April 2009
-
- Article
-
- You have access
- Export citation
REVERSE ITERATED FUNCTION SYSTEM AND DIMENSION OF DISCRETE FRACTALS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 79 / Issue 1 / February 2009
- Published online by Cambridge University Press:
- 09 February 2009, pp. 37-47
- Print publication:
- February 2009
-
- Article
-
- You have access
- Export citation
p-VARIATION OF VECTOR MEASURES WITH RESPECT TO BILINEAR MAPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 78 / Issue 3 / December 2008
- Published online by Cambridge University Press:
- 01 December 2008, pp. 411-430
- Print publication:
- December 2008
-
- Article
-
- You have access
- Export citation
A Compact Framework for Hidden Markov Chains with Applications to Fractal Geometry
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 45 / Issue 3 / September 2008
- Published online by Cambridge University Press:
- 14 July 2016, pp. 630-639
- Print publication:
- September 2008
-
- Article
-
- You have access
- Export citation
The Hausdorff dimension of a class of random self-similar fractal trees
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 39 / Issue 3 / September 2007
- Published online by Cambridge University Press:
- 01 July 2016, pp. 708-730
- Print publication:
- September 2007
-
- Article
-
- You have access
- Export citation
Renewal of singularity sets of random self-similar measures
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 39 / Issue 1 / March 2007
- Published online by Cambridge University Press:
- 01 July 2016, pp. 162-188
- Print publication:
- March 2007
-
- Article
-
- You have access
- Export citation
On Infinitesimal Increase of Volumes of Morphological Transforms
- Part of
-
- Journal:
- Mathematika / Volume 53 / Issue 1 / June 2006
- Published online by Cambridge University Press:
- 21 December 2009, pp. 103-127
- Print publication:
- June 2006
-
- Article
- Export citation
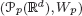 ). We prove that in most cases such a map is no more than 1/
). We prove that in most cases such a map is no more than 1/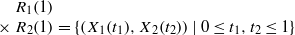 . The result of Hu generalizes [Some fractal sets determined by stable processes,
. The result of Hu generalizes [Some fractal sets determined by stable processes, 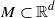 . An invariant set is defined to be a nonempty set
. An invariant set is defined to be a nonempty set 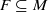 satisfying
satisfying 