Refine listing
Actions for selected content:
352 results in 28Axx
Pointwise multiple averages for sublinear functions
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 40 / Issue 6 / June 2020
- Published online by Cambridge University Press:
- 05 November 2018, pp. 1594-1618
- Print publication:
- June 2020
-
- Article
- Export citation
Delone dynamical systems and spectral convergence
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 40 / Issue 6 / June 2020
- Published online by Cambridge University Press:
- 22 October 2018, pp. 1510-1544
- Print publication:
- June 2020
-
- Article
- Export citation
ASYMPTOTIC LINEAR PROGRAMMING LOWER BOUNDS FOR THE ENERGY OF MINIMIZING RIESZ AND GAUSS CONFIGURATIONS
- Part of
-
- Journal:
- Mathematika / Volume 65 / Issue 1 / 2019
- Published online by Cambridge University Press:
- 27 September 2018, pp. 157-180
- Print publication:
- 2019
-
- Article
- Export citation
DEGENERATION OF ENDOMORPHISMS OF THE COMPLEX PROJECTIVE SPACE IN THE HYBRID SPACE
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 19 / Issue 4 / July 2020
- Published online by Cambridge University Press:
- 31 August 2018, pp. 1141-1183
- Print publication:
- July 2020
-
- Article
- Export citation
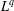 $L^{q}$-SPECTRUM OF SELF-SIMILAR MEASURES WITH OVERLAPS IN THE ABSENCE OF SECOND-ORDER IDENTITIES
$L^{q}$-SPECTRUM OF SELF-SIMILAR MEASURES WITH OVERLAPS IN THE ABSENCE OF SECOND-ORDER IDENTITIES
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 106 / Issue 1 / February 2019
- Published online by Cambridge University Press:
- 22 August 2018, pp. 56-103
- Print publication:
- February 2019
-
- Article
-
- You have access
- Export citation
ON THE WEAK-HASH METRIC FOR BOUNDEDLY FINITE INTEGER-VALUED MEASURES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 98 / Issue 2 / October 2018
- Published online by Cambridge University Press:
- 19 July 2018, pp. 265-276
- Print publication:
- October 2018
-
- Article
-
- You have access
- Export citation
BOX DIMENSION OF BILINEAR FRACTAL INTERPOLATION SURFACES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 98 / Issue 1 / August 2018
- Published online by Cambridge University Press:
- 30 May 2018, pp. 113-121
- Print publication:
- August 2018
-
- Article
-
- You have access
- Export citation
RANDOM SPARSE SAMPLING IN A GIBBS WEIGHTED TREE AND PHASE TRANSITIONS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 19 / Issue 1 / January 2020
- Published online by Cambridge University Press:
- 09 May 2018, pp. 65-116
- Print publication:
- January 2020
-
- Article
- Export citation
Assouad dimensions of complementary sets
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 148 / Issue 3 / June 2018
- Published online by Cambridge University Press:
- 12 April 2018, pp. 517-540
- Print publication:
- June 2018
-
- Article
- Export citation
A mass transference principle for systems of linear forms and its applications
- Part of
-
- Journal:
- Compositio Mathematica / Volume 154 / Issue 5 / May 2018
- Published online by Cambridge University Press:
- 03 April 2018, pp. 1014-1047
- Print publication:
- May 2018
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Recurrence to Shrinking Targets on Typical Self-Affine Fractals
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 61 / Issue 2 / May 2018
- Published online by Cambridge University Press:
- 15 February 2018, pp. 387-400
-
- Article
- Export citation
Local Fractal Interpolation on Unbounded Domains
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 61 / Issue 1 / February 2018
- Published online by Cambridge University Press:
- 23 January 2018, pp. 151-167
-
- Article
- Export citation
HAUSDORFF DIMENSION OF THE SET APPROXIMATED BY IRRATIONAL ROTATIONS
- Part of
-
- Journal:
- Mathematika / Volume 64 / Issue 1 / 2018
- Published online by Cambridge University Press:
- 14 February 2018, pp. 267-283
- Print publication:
- 2018
-
- Article
- Export citation
A UNIFIED APPROACH TO CONTINUOUS, MEASURABLE SELECTIONS, AND SELECTIONS FOR HYPERSPACES
- Part of
-
- Journal:
- Mathematika / Volume 64 / Issue 3 / 2018
- Published online by Cambridge University Press:
- 21 May 2018, pp. 607-627
- Print publication:
- 2018
-
- Article
- Export citation
ON THE
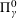 $\unicode[STIX]{x1D6F1}_{\unicode[STIX]{x1D6FE}}^{0}$ -COMPLETENESS AND
$\unicode[STIX]{x1D6F1}_{\unicode[STIX]{x1D6FE}}^{0}$ -COMPLETENESS AND 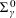 $\unicode[STIX]{x1D6F4}_{\unicode[STIX]{x1D6FE}}^{0}$ -COMPLETENESS OF MULTIFRACTAL DECOMPOSITION SETS
$\unicode[STIX]{x1D6F4}_{\unicode[STIX]{x1D6FE}}^{0}$ -COMPLETENESS OF MULTIFRACTAL DECOMPOSITION SETS
- Part of
-
- Journal:
- Mathematika / Volume 64 / Issue 1 / 2018
- Published online by Cambridge University Press:
- 06 February 2018, pp. 77-114
- Print publication:
- 2018
-
- Article
- Export citation
LIPSCHITZ EQUIVALENCE OF CANTOR SETS AND IRREDUCIBILITY OF POLYNOMIALS
- Part of
-
- Journal:
- Mathematika / Volume 64 / Issue 3 / 2018
- Published online by Cambridge University Press:
- 26 June 2018, pp. 730-741
- Print publication:
- 2018
-
- Article
- Export citation
DENSITY, SMITAL PROPERTY AND QUASICONTINUITY
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 97 / Issue 2 / April 2018
- Published online by Cambridge University Press:
- 04 December 2017, pp. 246-252
- Print publication:
- April 2018
-
- Article
-
- You have access
- Export citation
TWO-DIMENSIONAL SHRINKING TARGET PROBLEM IN BETA-DYNAMICAL SYSTEMS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 97 / Issue 1 / February 2018
- Published online by Cambridge University Press:
- 02 November 2017, pp. 33-42
- Print publication:
- February 2018
-
- Article
-
- You have access
- Export citation
COEFFICIENT ESTIMATES FOR SOME CLASSES OF FUNCTIONS ASSOCIATED WITH
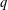 $q$ -FUNCTION THEORY
$q$ -FUNCTION THEORY
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 95 / Issue 3 / June 2017
- Published online by Cambridge University Press:
- 06 March 2017, pp. 446-456
- Print publication:
- June 2017
-
- Article
-
- You have access
- Export citation
Lacunary Interpolation by Fractal Splines with Variable Scaling Parameters
- Part of
-
- Journal:
- Numerical Mathematics: Theory, Methods and Applications / Volume 10 / Issue 1 / February 2017
- Published online by Cambridge University Press:
- 20 February 2017, pp. 65-83
- Print publication:
- February 2017
-
- Article
- Export citation
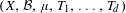
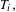
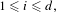
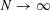
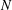
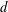
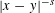
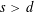
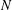
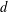
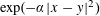
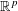
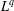
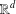
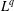
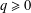
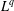
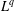

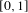
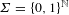

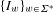
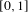
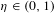
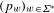
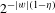
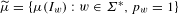
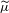
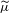

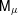
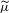

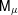

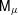

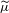

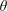
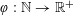


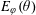

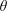
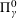
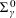
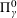
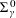
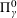
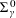
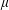
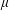
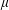
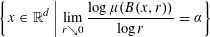
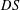
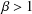
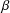
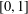
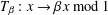
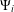
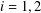
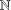
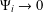
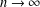
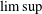
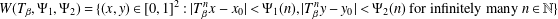
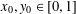
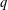
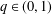







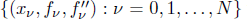 with equally spaced knot sequence in the unit interval, we show the existence of a family of fractal splines
with equally spaced knot sequence in the unit interval, we show the existence of a family of fractal splines 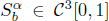 satisfying
satisfying 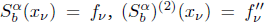 for
for 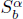 satisfies
satisfies 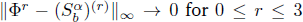 , as the number of partition points increases.
, as the number of partition points increases.